深度学习入门笔记 1
|
[CV] [Deep Learning]

https://www.bilibili.com/video/BV13b4y1177W

绪论

表示学习

机器学习的一般流程：

image-20250313170430872

浅层学习（shallow learning）：不涉及特征的学习，仅仅依靠人工经验或特征转换方法来抽取

特征处理：这里是人工完成的

特征可以分成（这里用图像举例）：

https://zhuanlan.zhihu.com/p/579717028

  • 底层特征：轮廓、边缘、颜色、纹理和形状特征。图像的低层的特征语义信息比较少，但是目标位置准确
  • 高层语义特征：值得是我们所能看的东西，比如对一张人脸提取低层特征我们可以提取到连的轮廓、鼻子、眼睛之类的，那么高层的特征就显示为一张人脸。高层的特征语义信息比较丰富，但是目标位置比较粗略。

语义的表示分为

  • 局部（符号）表示：离散表示、符号表示，如 One-Hot 向量
  • 分布式（distributed）表示：压缩的低维稠密向量

从局部（符号）映射到分布式表示称为嵌入（embedding）

表示学习：通过深度模型学习高层语义信息（也就是什么 loss 来梯度下降之类的）

image-20250313170720263

深度学习

一个好的表示学习策略必须具备一定的深度

深度学习=表示学习+浅层学习（也叫决策学习、预测学习）

image-20250313171226965

所有的东西都需要计算机自动来完成

核心问题：贡献度分配问题，即哪个结果影响最大

例子：

image-20250313171551379

上面的图中，逐步提取了底层特征、中层特征、高层特征，最后在分类器里面进行分类

这是个端到端（End-to-End）模型：中间没有人工干预。深度学习模型不一定是端到端模型

神经网络

下面是简单的人工神经元：

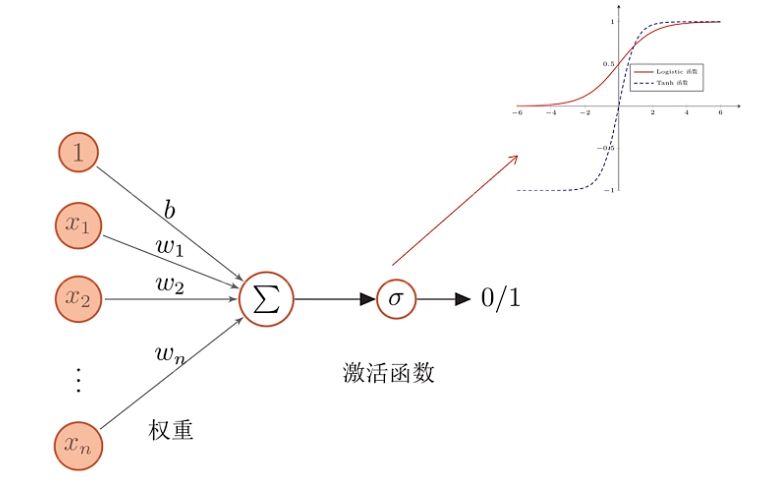
image-20250313172059173

其中，信号 $1$、$x_1$ 到 $x_n$ 被神经元按照 $b$、$w_1$ 到 $w_n$ 的权重接受（加权和），然后经过一个激活函数，最后产生一个新的信号

神经网络由大量的神经元以及它们之间的有向连接构成，因此需要考虑三方面：

  • 神经元的激活规则（激活函数）：神经元输入到输出的映射关系
  • 网络的拓扑结构：不同神经元之间的链接关系
  • 学习算法：训练的参数

神经网络根据结构大体分成三种：

  • 前馈网络：信息只向前传播
  • 记忆网络：有反馈边，在不同时刻有不同的状态（也就是记忆）
  • 图网络：网络结构是个图

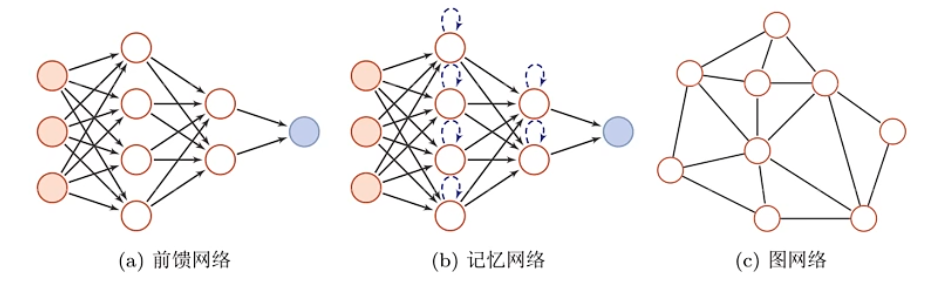
image-20250313172712292

大多数网络是一个复合结构

神经网络的每一层可以表示成：

$$ f^l(\vec x)=\sigma(W^lf^{l-1}(\vec x)) $$

神经网络可以解决贡献度分配问题：

$$ \frac{\partial y}{\partial W^l}=\frac{y(W^l+\Delta W)-y(W^l)}{\Delta W} $$

（这里之后要再看）

我们可以发现，假如某个参数非常重要，那么如果对这个参数做一个扰动，会对结果产生很大的影响。这样就可以调整贡献度分配了

机器学习

机器学习就是自动构建一个映射函数，即从大量数据中学习一般性规律，并且使用这些规律来对未知数据进行预测

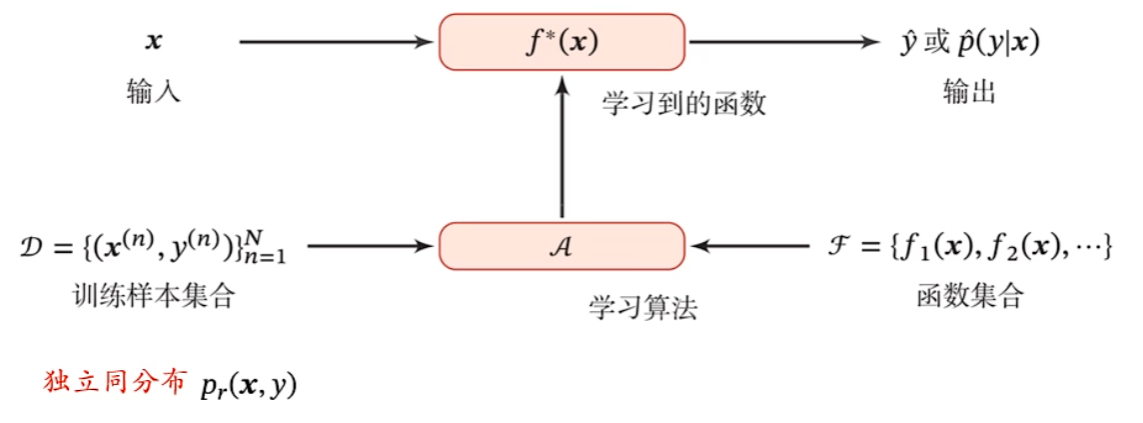
image-20250313174844829

机器学习的分类

根据学习的方法可以分成三类：

监督学习无监督学习强化学习
训练样本训练集 $\{(\vec x^{(n)},y^{(n)})\}_{n-1}^N$训练集 $\{(\vec x^{(n)})\}_{n-1}^N$智能体与环境交互的轨迹 $\tau$ 和累积奖励 $G_\tau$
优化目标$y=f(\vec x)$ 或 $p(y\vert\vec x)$$p(\vec x)$ 或带隐变量 $\vec z$ 的 $p(\vec x\vert\vec z)$期望总回报 $\mathbb E_\tau[G_\tau]$
学习准则期望风险最小化
最大似然估计		最大似然估计
最小重构错误		策略评估
策略改进

还可以结合起来：半监督学习

还有：半监督学习、弱监督学习等

两个典型的监督学习问题：

  • 回归（regression）问题：给定输入变量（特征），输出一个连续值
  • 分类（classification）问题：给定输入变量（特征），输出一个离散值

典型的无监督学习问题：

  • 聚类问题
  • 降维问题
  • 密度估计

机器学习的四个要素

数据、模型、学习准则、优化算法

模型其实就是一个函数，如线性回归任务：

$$ f(\vec x;\theta)=\mathbf w^T\vec x+b $$

其中，$\mathbf w^T$ 和 $b$ 是要学习的参数，$\theta$ 是所有要学习的参数总称

非线性回归任务：

$$ f(\vec x;\theta)=\mathbf w^T\phi(\vec x)+b $$

其中，$\phi$ 是一个非线性基函数，如果它是可学习的，就可以把这个函数看做神经网络

学习准则是学习的目标，一个好的模型应该在所有取值上都与真实映射函数一致

这就涉及到损失函数（loss function）：一个非负实函数，量化预测值与真实值的差异。例如平方损失函数（quadratic loss function）：

$$ \mathcal L(y,f(\vec x,\theta))=\frac{1}{2}\left(y-f(\vec x,\theta)\right)^2 $$

在定义完损失函数之后，还有期望风险（expected risk）：

$$ \mathcal R(\theta)=\mathrm E_{(\vec x,y)\sim p_r(\vec x,y)}[\mathcal L\left(y,f(\vec x,\theta)\right)] $$

其中，$p_r(\vec x,y)$ 是真实的数据分布，$\mathcal L$ 是损失函数

这个值是无法计算的，根据大数定律，可以近似为：

$$ \mathcal R_{\mathcal D}^{\text{emp}}(\theta)=\frac{1}{N}\sum_{n=1}^N\mathcal L\left(y^{(n)},f(\vec x^{(n)},\theta)\right) $$

这个叫做经验风险（empirical risk）

然后我们就只要最小化经验风险即可，这样机器学习问题就转化成了最优化问题

优化算法指的就是最优化问题的方法，例如梯度下降法：

$$ \theta_{t+1}=\theta_t-\alpha\frac{\partial \mathcal R_\mathcal D(\theta)}{\partial \theta} $$

其中步长 $\alpha$ 称为学习率，是个超参数，后面是梯度

改进：随机梯度下降、小批次梯度下降

泛化与正则化

欠拟合、过拟合问题：

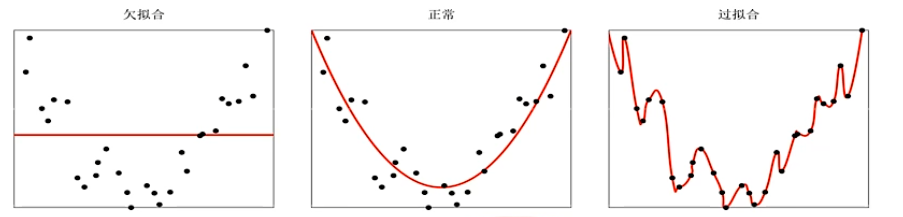
image-20250313193227104

过拟合问题的原因：训练数据少、噪声等

所以机器学习不等价为优化问题，因为期望风险不等价于经验风险，差异称为泛化误差：

$$ \mathcal G_\mathcal D(f)=\mathcal R(f)-\mathcal R_\mathcal D^{\text{emp}}(f) $$

通过正则化（regularizayion，降低模型复杂度）的方法可以减少泛化误差

所有损害优化的方法都是正则化，如：

  • 增加优化约束：L1/L2 约束、数据增强
  • 干扰优化过程：权重衰减、随机梯度下降、提前停止（使用验证集测试，如果错误率不降低就停止迭代）

线性回归和多项式回归

最小二乘法

避免不可逆问题，加入结构风险作为正则化项：

$$ \mathcal{\hat R}(\mathbf w)=\frac{1}{2}\Vert \vec y-\mathbf X^T\mathbf w\Vert^2+\frac{1}{2}\lambda\Vert\mathbf w\Vert^2 $$

其中，$\lambda$ 叫做正则化系数。此时最小化得到：

$$ \mathbf w^*=(\mathbf X\mathbf X^T+\lambda \mathbf I)^{-1}\mathbf X\vec y $$

此时叫做结构风险最优化

多项式曲线拟合（polynomial curve fitting），多项式的次数 $M$ 是一个超参数

加入正则化项来惩罚大系数

可以通过增大样本数量来避免过拟合

线性模型

线性分类模型：二分类与多分类

交叉熵：

在信息论中，熵（entropy）用来衡量随机事件的不确定性。熵越高随机变量的信息越多，熵越低随机变量的信息越少

自信息（self information）：一个随机事件中包含的信息量

对于随机变量 $X$，当 $X=x$ 时自信息定义为：

$$ I(x)=-\log p(x) $$

熵此时可以定义为随机变量 $X$ 的自信息的数学期望：

$$ H(x)=\mathrm E_X[I(x)]=\mathrm E_X[-\log p(x)]=-\sum_{x\in X}p(x)\log p(x) $$

熵编码（entropy encoding）：使用自信息进行编码，即对于 $x\in X$，如果分布函数为 $p$，那么熵编码为：

$$ -\log p(x) $$

交叉熵（cross entropy）：按照概率分布 $q$ 的最优编码对真实分布为 $p$ 的信息进行编码的长度

$$ H(p,q)=\mathrm E_p[-\log q(x)]=-\sum_{x}p(x)\log q(x) $$

KL 散度（Kullback-Leibler divergence）是用概率分布 $q$ 来近似 $p$ 时所造成的信息损失量

$$ \mathrm{KL}(p,q)=H(p,q)-H(p)=\sum_{x}p(x)\log\frac{p(x)}{q(x)} $$

交叉熵损失、负对数似然

前馈神经网络

神经元

人工神经元如下：

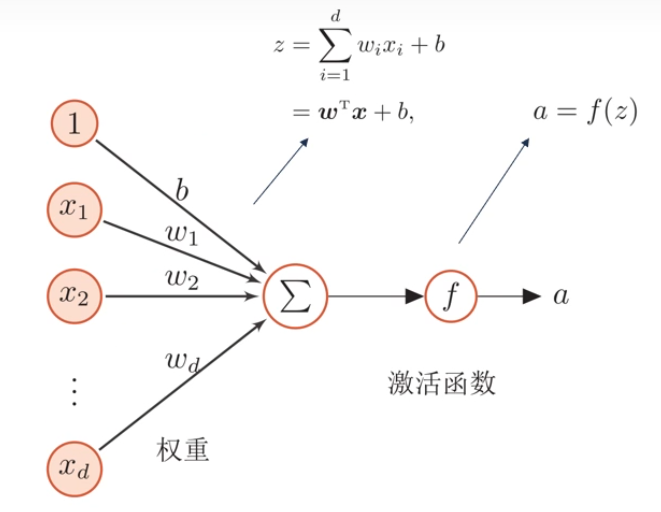
image-20250313202456628

这是一个简单的线性模型

其中，激活函数有很多，它需要满足一些性质：

  • 连续可导（允许少数点上不可导）的非线性函数，方便使用数值优化的方法来学习网络参数
  • 激活函数及其导函数尽可能简单，以提高网络计算效率
  • 激活函数的导函数的值域要在一个合适的区间内（不能太大也不能太小）

常用的激活函数：

  • S 型函数（Sigmoid function）
  • 斜坡函数（ramp function）
  • 复合函数（compound function）

S 型函数举例：

Logistics 函数：

$$ \sigma(x)=\frac{1}{1+e^{-x}} $$

$\tanh$ 函数：

$$ \tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} $$

它们有下面的关系：

$$ \tanh(x)=2\sigma(2x)-1 $$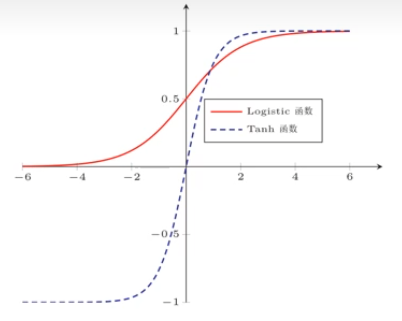

image-20250313203355891

性质：

  • 这两个函数都是饱和函数（两边梯度接近 $0$）
  • $\tanh$ 函数是零中心化的，而 Logistics 函数的输出恒大于 $0$

非零中心化的输出会使后一层神经元的输入发生偏置偏移 bias shift，使得收敛速度变慢

斜坡函数举例：

ReLU 函数：

$$ \mathrm{ReLU}(x)=\max(0,x) $$

它计算高效，生物学合理，一定程度上缓解梯度消失问题

但是有死亡 ReLU 问题（dying ReLU problem）

改进方法：LeakyReLU 函数：

$$ \mathrm{LeakyReLU }(x)=\max(0,x)+\gamma\min(0,x) $$

近似的零中心化的非线性函数：

$$ \mathrm{ELU}(x)=\max(0,x)+\min(0,\gamma(e^x-1)) $$

Rectifier 函数的平滑版本：

$$ \mathrm{Softplus}(x)=\log(1+e^x) $$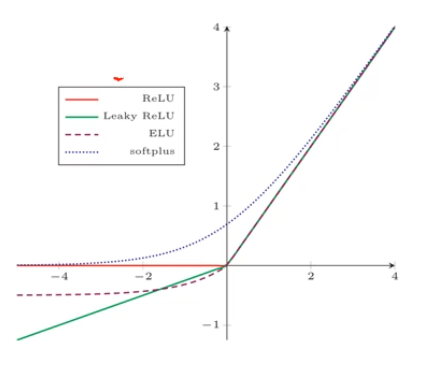

image-20250313203717862

复合函数举例：

Swish 函数：一种自门控（Self-Gated）激活函数

$$ \mathrm{swish}(x)=x\sigma(\beta x) $$

高斯误差线性单元（Gaussian Rrror Linear Unit，GELU）：

$$ \mathrm{GELU}(x)=xP(X\le x) $$

其中，$P(X\le x)$ 是高斯分布 $N(\mu,\sigma^2)$ 的累积分布函数，$\mu$ 和 $\sigma$ 是超参数

它可以用 $\tanh$ 函数或者 Logistic 函数来近似

前馈神经网络

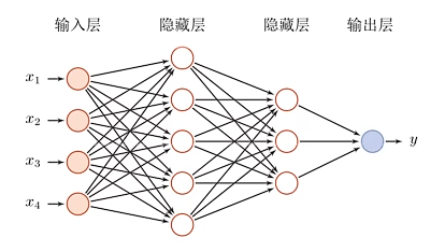
image-20250313205413950

记号含义
$L$层数
$M_l$第 $l$ 层神经元个数
$f_l(\cdot)$第 $l$ 层神经元的激活函数
$\mathbf W^T\in\mathbb R^{M_l\times M_{l-1}}$第 $l-1$ 层到第 $l$ 层的权重矩阵
$\vec b^{(l)}\in\mathbb R^{M_l}$第 $l-1$ 层到第 $l$ 层的偏置
$\vec z^{(l)}\in\mathbb R^{M_l}$第 $l$ 层神经元的净输入（纯活性值）
$\vec a^{(l)}\in\mathbb R^{M_l}$第 $l$ 层神经元的输出（活性值）

那么有：

$$ \displaylines{ \vec z^{(l)}=\mathbf W^T\vec a^{(l-1)}+\vec b^{(l)}\\ \vec a^{(l)}=f_l(\vec z^{(l)}) } $$

前馈计算就是：

$$ \vec x=\vec a^{(0)}\rightarrow\vec z^{(1)}\rightarrow\vec a^{(1)}\rightarrow\cdots\rightarrow\vec z^{(L)}\rightarrow\vec a^{(L)}\rightarrow\phi(\vec x;\theta) $$

通用近似定理：神经网络可以近似任何的函数

Softmax 函数是一种特殊的激活函数

关于多分类问题：

  • 最后一层的多个神经元经过 Softmax 归一化后可以作为条件概率
  • 采用交叉熵损失函数，即：$\mathcal L(\vec y,\hat{\vec y})=-\vec y^T\log\hat{\vec y}$

结构化风险函数：

$$ \mathcal{\hat R}(\mathbf W)=\frac{1}{N}\sum_{n=1}^N\mathcal L(\vec y^{(n)},\hat{\vec y}^{(n)})+\frac{1}{2}\lambda\Vert\mathbf W\Vert^2_F $$

其中，$\Vert\mathbf W\Vert^2_F$ 叫做 Forbenius 范数：

$$ \Vert\mathbf W\Vert^2_F=\sum_{l=1}^{L}\sum_{i=1}^{M_l}\sum_{j=1}^{M_{l-1}}\left(w_{ij}^{(l)}\right)^2 $$

梯度下降：计算对于每一层的 $\mathbf W$ 和每一层的 $\vec b$ 即可

神经网络为一个复杂的复合函数，需要使用链式法则来计算偏导数

下面会介绍反向传播算法

还有更通用的自动微分方法（Automatic Differentiation，AD）

反向传播

矩阵微积分（matrix calculus）：标量关于向量的偏导数、向量关于向量的偏导数、链式法则（注意顺序）

需要对于结构化风险函数进行求导，因为正则化项求导较为简单，所以略过它，只求前面的：

$$ \begin{aligned} \frac{\partial\mathcal L(\vec y^{(n)},\hat{\vec y}^{(n)})}{\partial w_{ij}^{(l)}}&=\frac{\partial\vec z^{(l)}}{\partial w_{ij}^{(l)}}\frac{\partial\mathcal L(\vec y^{(n)},\hat{\vec y}^{(n)})}{\partial\vec z^{(l)}}\\ \frac{\partial\mathcal L(\vec y^{(n)},\hat{\vec y}^{(n)})}{\partial \vec b^{(l)}}&=\frac{\partial\vec z^{(l)}}{\partial\vec b^{(l)}}\frac{\partial\mathcal L(\vec y^{(n)},\hat{\vec y}^{(n)})}{\partial\vec z^{(l)}} \end{aligned} $$

对于每个式子前面那一项，可以得到：

$$ \begin{aligned} \frac{\partial\vec z^{(l)}}{\partial w_{ij}^{(l)}}&=[0,\cdots,a_j^{(l-1)},\cdots,0]\in\mathbb R^{1\times M_l} \\ \frac{\partial\vec z^{(l)}}{\partial\vec b^{(l)}}&=\mathbf I_{M_l}\in\mathbb R^{M_l\times M_l} \end{aligned} $$

后面的项是误差项，记作 $\delta^{(l)}\in \mathbb R^{M_l}$，可以算出：

$$ \delta^{(l)}=f_l'(\vec z^{(l)})\odot \left((\mathbf W^{(l+1)})^T\delta^{(l+1)}\right) $$

其中，$\odot$ 表示逐元素乘。这个过程就叫做反向传播

我们可以合起来：

$$ \begin{aligned} \frac{\partial\mathcal L(\vec y^{(n)},\hat{\vec y}^{(n)})}{\partial \mathbf W^{(l)}}&=\delta^{(l)}(\vec a^{(l-1)})^T\in\mathbb R^{M_l\times M_l}\\ \frac{\partial\mathcal L(\vec y^{(n)},\hat{\vec y}^{(n)})}{\partial \vec b^{(l)}}&=\delta^{(l)}\in \mathbb R^{M_l} \end{aligned} $$

计算图与自动微分

自动微分是利用链式法则来自动计算一个复合函数的梯度

计算图：

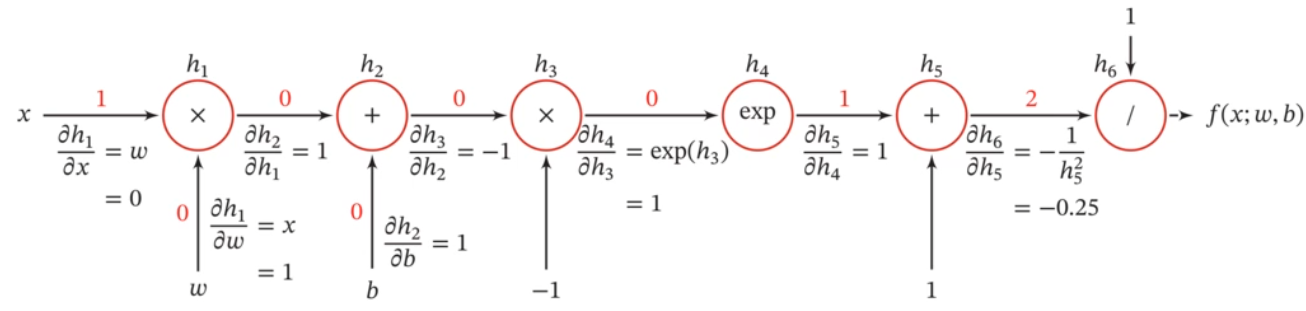
image-20250314123702725

自动微分分为反向模式和前向模式

静态计算图（tensorflow）与动态计算图（pytorch）

优化问题

非凸优化问题：全局最优与局部最优问题、鞍点问题

梯度消失问题（vanishing gradient problem）：链式法则计算后期梯度趋近为 $0$

卷积神经网络

局部不变性特征：尺度缩放、平移、旋转等操作不影响其语义信息

全连接前馈网络的参数非常多，很难提取这些局部不变特征

卷积神经网络（convolutional neural networks，CNN）是一种前馈神经网络，有三个结构上的特征：

  • 局部连接
  • 权重共享
  • 空间或时间上的次采样

卷积

给定信号序列 $x$ 和滤波器 $w$，卷积的输出为：

$$ y_t=\sum_{k=1}^Kw_kx_{t-k+1} $$

其中，$w$ 称为卷积核（convolutional kernel）或滤波器（filter）

如果卷积核长度为 $K$，输入长度为 $N$，那么输出长度就是 $N-K+1$

作用：近似微分、低通或高通滤波

引入滑动步长 $S$ 和零填充 $P$

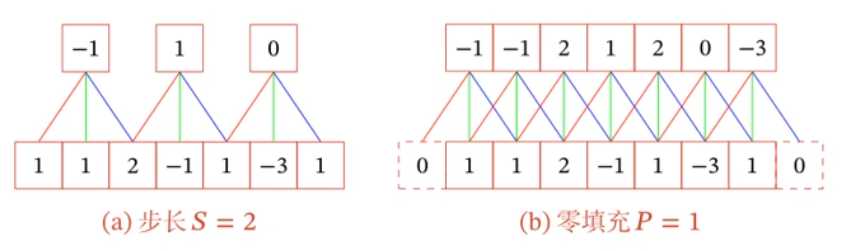
image-20250314125808136

窄卷积、宽卷积、等宽卷积（目前文献中默认）

二维卷积：

$$ \mathbf Y=\mathbf W*\mathbf X $$

即：

$$ y_{ij}=\sum_{u=1}^U\sum_{v=1}^Vw_{uv}x_{i-u+1,j-v+1} $$

二维卷积可以作为特征提取器

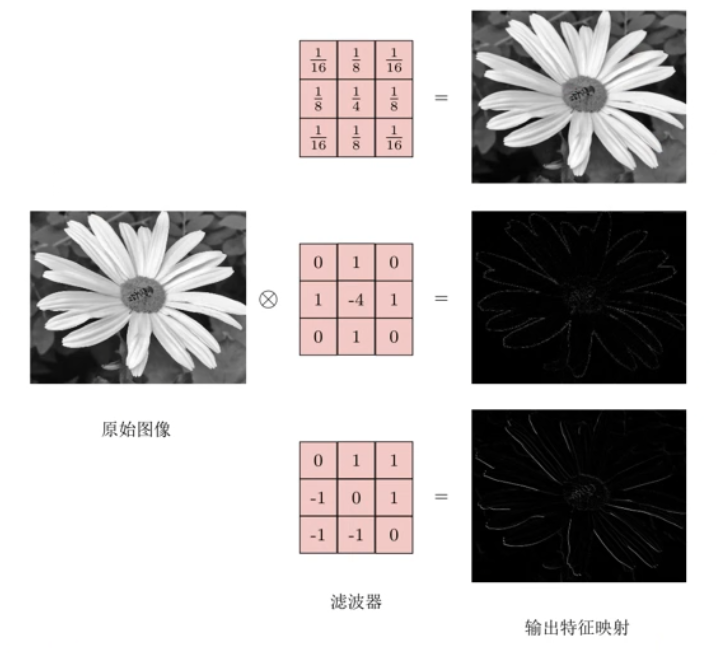
image-20250314130457643

如果卷积核是一个可学习的参数，那么就叫做卷积神经网络

空洞卷积（增加感受野）、转置卷积或微步卷积（低维特征映射到高维特征）

卷积神经网络

用卷积层代替全连接层

互相关：计算卷积需要进行卷积核反转，这个反转是不必要的，取消这个反转就叫做互相关

一般来说，这里的卷积都是互相关

引入多个卷积核来增强卷积层的能力。

特征映射（feature map）：图像经过卷积后得到的特征

卷积层的输入输出一般为：

  • 输入：$D$ 个特征映射 $M\times N\times D$
  • 输出：$P$ 个特征映射 $M'\times N'\times P$

其中，$D$ 和 $P$ 叫做深度或者通道数

卷积层的映射关系（对于第 $P$ 个特征映射）

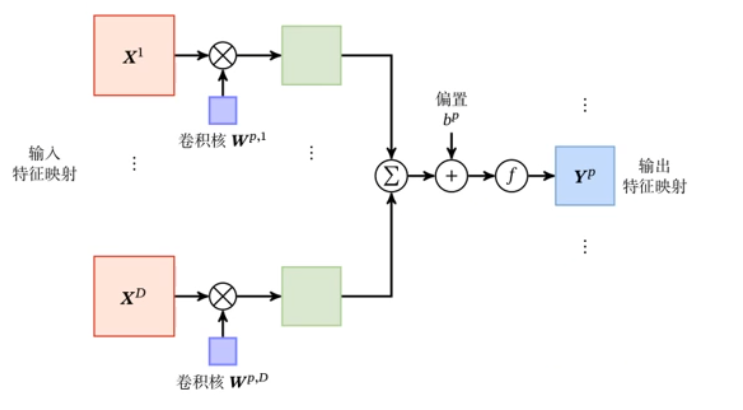
image-20250314134101427

也就是：

$$ \begin{aligned} \mathbf Z^P&=\mathbf W^P\otimes\mathbf X+b^P=\sum_{d=1}^D\mathbf W^{P,d}\otimes\mathbf X+b^P\\ \mathbf Y^P&=f(\mathbf Z^P) \end{aligned} $$

这是一个典型的卷积层，可以看成是三维结构：

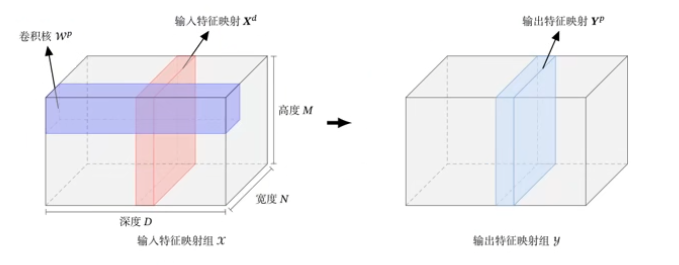
image-20250314134622382

汇聚层（pooling layer）或者叫池化层：卷积层虽然可以显著减少连接的个数，但是每个特征映射的神经元个数并没有显著减少

汇聚层（pooling layer）要做的事就是降采样

最常用的叫最大汇聚（max pooling），还有平均汇聚

卷积神经网络有卷积层、汇聚层、全连接层交叉堆叠而成：

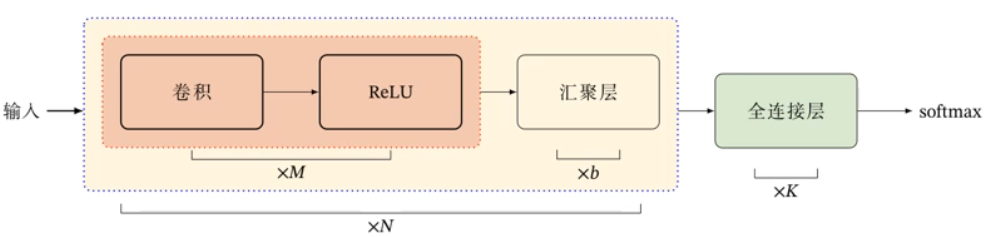
image-20250314135008096

典型结构：

  • 趋向于小卷积、大深度
  • 趋向于全卷积

典型的 CNN：

  • LeNet
  • AlexNet：第一个现代深度卷积网络模型
  • GoogLeNet：由多个 inception 模块和少量汇聚层堆叠而成
  • ResNet（Residual Network）：残差网络，152 层的深层网络。通过给非线性的卷积层增加直连边（shortcut connection）来提高信息的传播效率

inception 模块 v1：

卷积网络中，如何设置卷积层的卷积核大小十分关键，在 inception 模块中，包含多个不同大小的卷积操作：

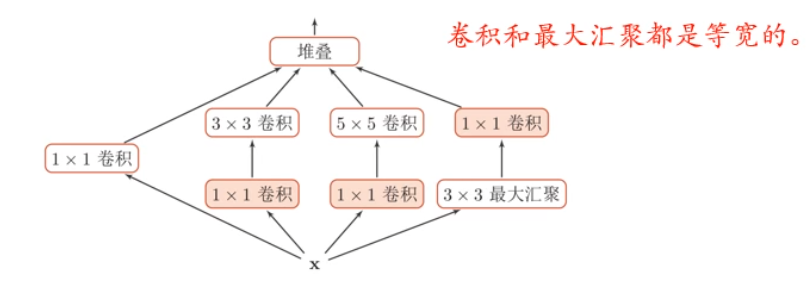
image-20250314141801056

inception 模块 v3：

用多层小卷积核替换大卷积核，以减少计算量和参数量

  • 用两层 $3\times 3$ 卷积来替换 v1 中 $5\times5$ 卷积
  • 用连续的 $n\times 1$ 卷积和 $1\times n$ 卷积来 v1 中 $n\times n$ 卷积

残差网络的残差单元：

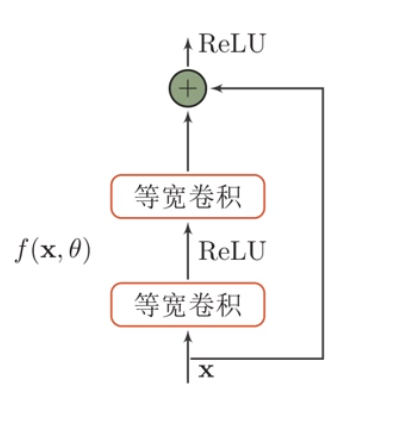
image-20250314142856445

即：

$$ h(\vec x)=\vec x+f(\vec x,\theta) $$

这样，由于偏导数有一个常数 $1$，所以偏导数不会很小，它可以堆得很深

还有：区域卷积神经网络（RCNN）

循环神经网络

优点：引入（短期）记忆、图灵完备

缺点：长程依赖问题、记忆容量问题、并行能力

给神经网络增加记忆能力

前面的神经网络没有记忆功能

时延神经网络（Time Delay Neural Network，TDNN）：建立一个额外的延时单元：

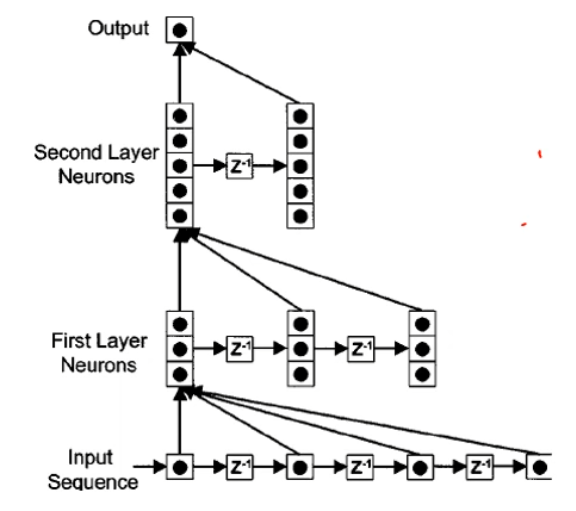
image-20250314145030197

实际上就是：

$$ \vec {h}_t^{(l)}=f(\vec {h}_{t}^{(l)},\vec {h}_{t-1}^{(l)},\cdots,\vec {h}_{t-K}^{(l)}) $$

自回归模型（Autoregressive Model，AR）：

$$ \vec{y}_t=w_0+\sum_{k-1}^Kw_k\vec{y}_{t-k}+\epsilon_t $$

其中，$\epsilon_t\sim N(0,\sigma^2)$ 是第 $t$ 时刻的噪声

有外部输入的非线性自回归模型（Nonlinear Autoregressive with Exogenous Inputs Model，NARX）：

$$ \vec{y}_t=f(\vec{x}_t,\vec{x}_{t-1},\cdots,,\vec{x}_{t-K_x},\vec{y}_{t-1},\vec{y}_{t-2},\cdots,\vec{y}_{t-K_y}) $$

其中，$K_x$ 与 $K_y$ 为超参数，$f(\cdot)$ 是一个非线性函数，可以是一个前馈网络

循环神经网络

循环神经网络（Recurrent Neural Network，RNN）通过使用带自反馈的神经元，能够处理任意长度的时序数据

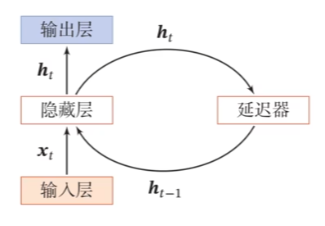
image-20250314145932863

其中：

$$ \vec h_t=f(\vec h_{t-1},\vec x_t) $$

$\vec h_t$ 叫做活性值状态

它比前馈神经网络更符合生物神经网络的结构

简单循环网络（Simple Recurrent Network，SRN）：

$$ \vec h_t=f(\mathbf U\vec h_{t-1}+\mathbf W\vec x_t+\vec b) $$

通用近似定理

应用到机器学习：

  • 正常模式
  • 按时间进行平均采样模式
  • 同步的序列到序列模式
  • 异步的序列到序列模式：左边叫做编码器，右边叫做解码器

image-20250314151916194

参数学习和长程依赖问题

假设使用同步的序列到序列模式，它的瞬时损失函数为：

$$ \mathcal L_t=\mathcal L(y_t,g(\vec h_t)) $$

其中，$y_t$ 表示真实值，后面的是预测值。

总的损失函数是：

$$ \mathcal L=\sum_{t=1}^T\mathcal L_t $$

它也可以反向传播，这里就不细看了：

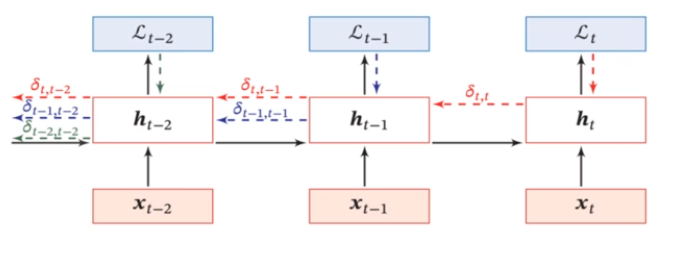
image-20250314172856387

对于简单循环神经网络，它的误差项是：

$$ \delta_{t,k}=\prod_{\tau=k}^{t-1}\left(\mathrm{diag}(f'(\vec z_\tau)\mathbf U^T)\right)\delta_{t,t} $$

为了方便研究，我们将其近似为：

$$ \delta_{t,k}\cong\gamma^{t-k}\delta_{t,t} $$

当 $\gamma$ 大于 $1$ 时会发生梯度爆炸，当 $\gamma$ 小于 $1$ 时会发生梯度消失（$t-k\to\infty$ 时），这个问题可以统称为长程依赖问题（long-term dependencies problem），实际上只能学习到短周期的依赖关系

如何改进？

  • 梯度爆炸问题（相对容易解决）：权重衰减、梯度截断
  • 梯度消失问题：改进模型（循环边改成线性依赖关系、增加非线性（类似于残差网络））

GRU 和 LSTM

门控机制：控制信息的累积速度，包括有选择地加入新的信息，并有选择地遗忘之前累积的信息

基于门控的循环神经网络（Gated RNN）：门控循环单元（Gated Recurrent Unit，GRU）、长短期记忆网络（long short-term memory，LSTM）

我们前面使用增加非线性的方式改进模型：

$$ \vec h_t=\vec h_{t-1}+g(\vec x_t,\vec h_{t-1};\theta) $$

随着训练，$\vec h$ 可能会越来越大，从而使得后面的非线性函数出现饱和现象，套上激活函数之后趋近于 $1$

为了不让它变得这么大，引入某种遗忘机制：

$$ \vec h_t=\vec z_t\odot\vec h_{t-1}+(1-\vec z_t)g(\vec x_t,\vec h_{t-1};\theta) $$

其中，$\vec z_t\in (0,1)^d$，它叫做更新门，控制两个之间的比例

更新门的实现可以使用 Logistics 函数：

$$ \vec z_t=\sigma(\mathbf W_z\vec x_t+\mathbf U_z\vec h_{t-1}+\vec b_z) $$

后面的 $g(\cdot)$ 可以使用 $\tanh$ 实现（这里记为 $\tilde {\vec h}_t$）：

$$ \tilde {\vec h}_t=\tanh(\mathbf W_h\vec x_t+\mathbf U_h\vec h_{t-1}+\vec b_h) $$

然后我们发现，当前的公式没法做到模型只与 $\vec x_t$ 相关，于是引入一个重置门 $\vec r_t$：

$$ \begin{aligned} \vec r_t&=\sigma(\mathbf W_r\vec x_t+\mathbf U_r\vec h_{t-1}+\vec b_r)\\ \tilde {\vec h}_t&=\tanh(\mathbf W_h\vec x_t+\mathbf U_h(\vec r_t\odot\vec h_{t-1})+\vec b_h) \end{aligned} $$

这样就构成了一个门控循环单元：

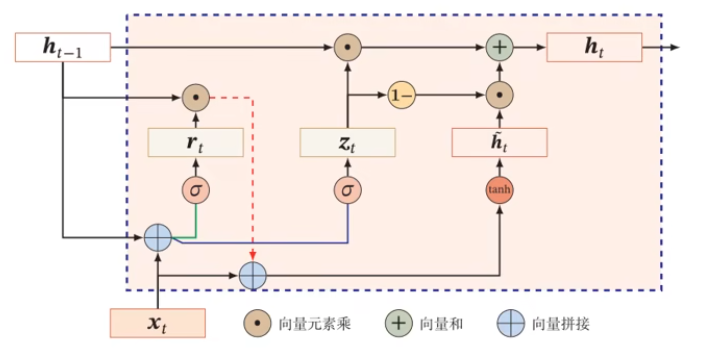
image-20250314175614712

LSTM 的结构如下：

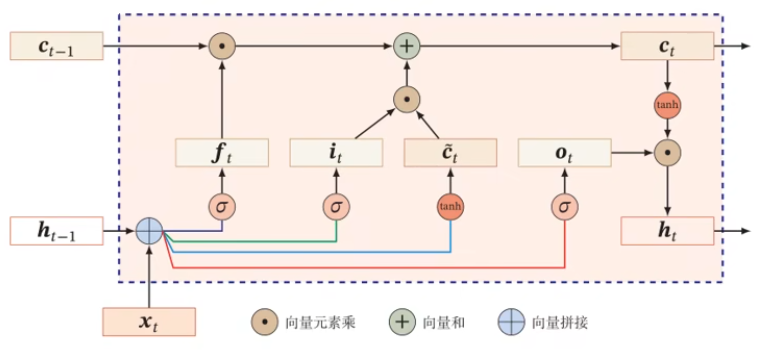
image-20250314175922091

它引入了新的内部记忆单元 $\vec c$，来做线性，从而释放出 $\vec h$，让它可以更好地做非线性工作：

$$ \begin{aligned} \tilde {\vec c}_t&=\tanh(\mathbf W_c\vec x_t+\mathbf U_c\vec h_{t-1}+\vec b_c)\\ \vec c_t&=\vec f_t\odot\vec c_{t-1}+\vec i_t\odot\tilde {\vec c}_t \end{aligned} $$

$\vec i_t$ 和 $\vec f_t$ 计算和前面差不多，然后得到 $\vec h_t$：

$$ \vec h_t=\vec o_t\odot\tanh(\vec c_t) $$

耦合输入门和遗忘门、peephole 连接

深层循环神经网络

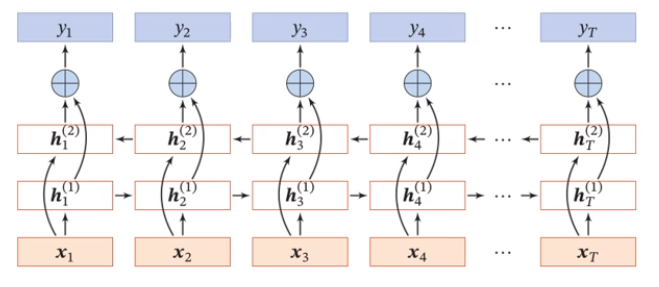
堆叠（stacked）循环神经网络：

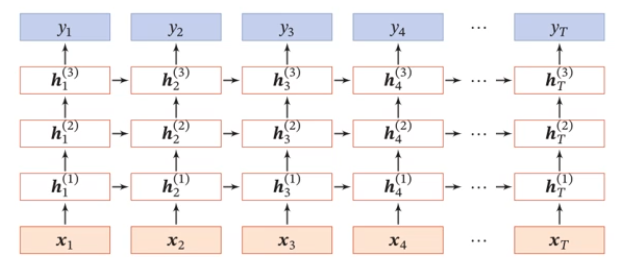
image-20250314180942284

双向循环神经网络：

image-20250314181104648

Milk Feng
May all the beauty be blessed
随笔归档 | Archives 个人简历 | Resume
 
       

Hugo Theme Diary by Rise
移植自 Makito's Journal.

© Milk Feng - CC BY-NC 4.0