https://www.bilibili.com/video/BV19u411d7r3

网络优化与正则化

难点：

• 结构差异大：没有通用优化算法、超参数多
• 非凸优化问题：参数初始化、逃离局部最优或鞍点
• 梯度消失或梯度爆炸问题

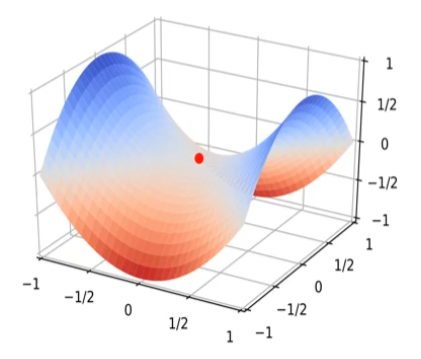
鞍点（saddle point）：在某些维度下是局部最小点，某些维度下是局部最大点

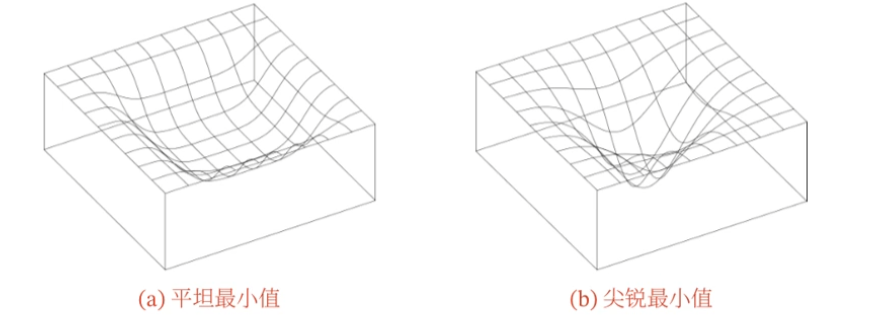
平坦最小值（flat minima）：

• 在一个平坦最小值的邻域内，所有点的训练损失都比较接近
• 大部分的局部最小解是等价的
• 局部最小解对应的训练损失都可能非常接近全局最小解的训练损失

这导致我们可能并不需要找到全局最优解，只需要找到局部最小解

优化地形（optimization landscape）

残差网络可以缓解梯度消失问题，也会使得优化地形更加平缓，优化效率更高

神经网络优化的改善方法：

• 更有效的优化算法来提高效率和稳定性：动态学习率调整、梯度估计修正
• 更好的参数初始化方法、数据预处理方法来提高优化效率
• 修改网络结构来得到更好的优化地形：ReLU、残差连接、逐层归一化
• 使用更好的超参数优化方法

批量大小

小批量随机梯度下降中的批量大小：

• 批量大小不影响随机梯度的期望，但会影响随机梯度的方差（批量越大，方差越小）
• 批量较小时需要设置较小的学习率，否则模型不会收敛
• 批量大小和学习率的关系：线性缩放规则
• 小的批量大小泛化性更好，大的批量大小优化效率更高，小的批量大小迭代快

学习率调整与梯度估计修正

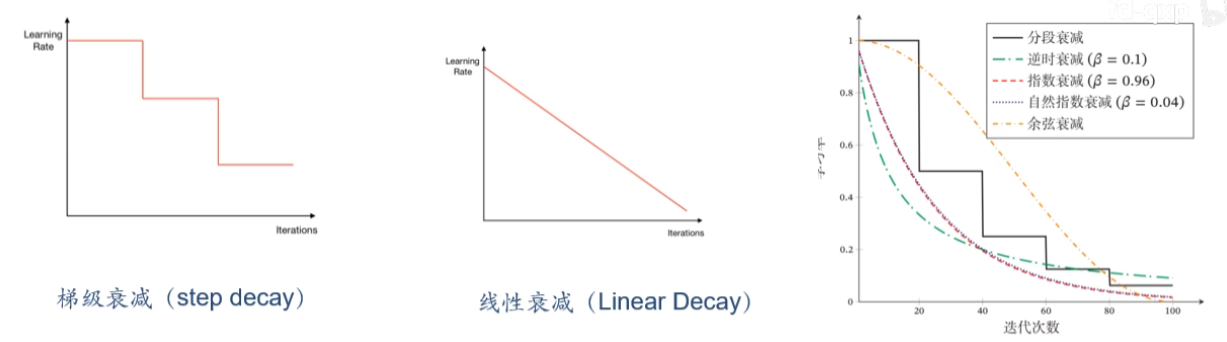
学习率衰减：

• 梯级衰减（step decay）
• 线性衰减（linear decay）
• 逆时衰减（inverse time decay）：$\alpha_t=\alpha_0\frac{1}{1+\beta\times t}$
• 指数衰减（exponential decay）：$\alpha_t=\alpha_0\beta^t$
• 自然指数衰减（natural exponential decay）：$\alpha_t=\alpha_0e^{-\beta\times t}$
• 余弦衰减（cosine decay）：$\alpha_t=\frac{1}{2}\alpha_0(1+\cos(t\pi/T))$

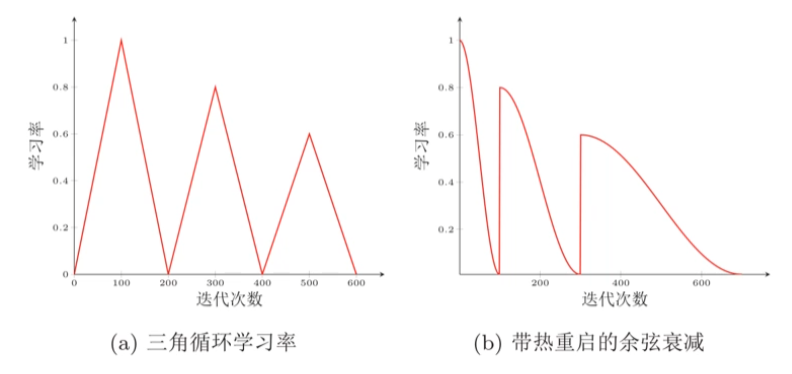
周期性学习率调整（cyclical learning rate）：

学习率优化的其他方法：

• 增大批量大小
• 学习率预热（warmup）：

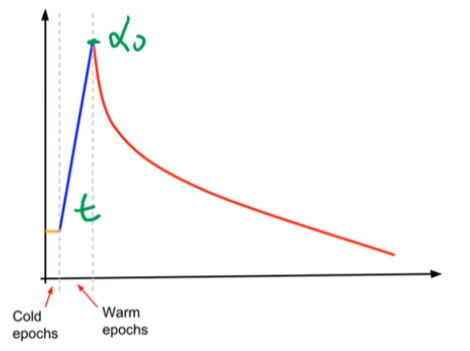
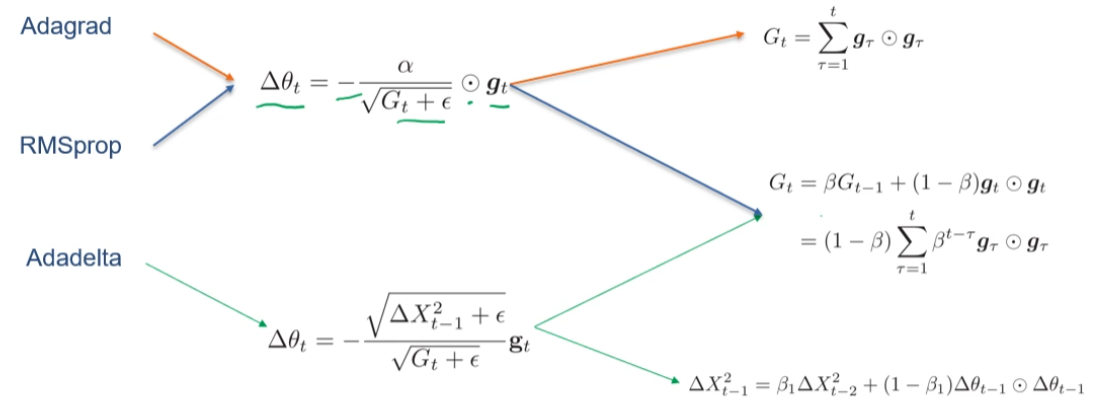
自适应学习率：

梯度方向优化：

• 动量法（momentum method）：用累积动量来替代真正的梯度
• Nesterov 加速梯度
• 梯度截断：把梯度的模限定在一个区间

综合方法：

• Adam 算法：约等于动量法 + RMSprop（梯度方向优化 + 自适应学习率）

大部分优化算法可以使用下面的公式来统一概况：

其中，$\vec g_t$ 是第 $t$ 步的梯度

参数初始化与数据预处理

初始化方法：

• 预训练初始化
• 随机初始化：
  • Gaussian 分布初始化：最简单，高斯分布
  • 均匀分布初始化：$[-r,r]$ 内均匀分布
  • 范数保持性（Norm-Perserving）：权重矩阵尽量为正交矩阵
    • 基于方差缩放的参数初始化：Xavier 初始化和 He 初始化
    • 正交初始化
• 固定值初始化（例如使用 $0$ 来初始化偏置值）

要通过优化来反推随机初始化的参数（例如方差、$r$）

尺度不变性（scale invariance）：算法在缩放全部或部分特征后不影响学习和预测

如果数据没有规范化会对梯度产生影响

规范化（normalization）：

• 最大最小值规范化
• 标准化
• PAC

神经网络的逐层规范化：

• 可以有更好的尺度不变性，解决内部协变量偏移
• 更平滑的优化地形

规范化方法：

• 批量规范化（Batch Normalization，BN）
• 逐层规范化
• 权重规范化
• 局部响应规范化