3DGS 1. 高斯分布与高斯椭球

§ 参考资料共 11 条

3DGS 全称 3D Gaussian Splatting，其中的“Gaussian”就是高斯分布，这是在物理学中的叫法，它还有一个通用的名称，叫做正态分布

3DGS 中的高斯分布是三维的

一元高斯分布

若一个随机变量服从一个平均数为 $\mu$，标准差为 $\sigma$ 的高斯分布，则记作：

$$ X\sim N(\mu,\sigma^2) $$

它的概率密度函数为：

$$ f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} $$

若 $\mu=0$ 且 $\sigma=1$，则称 $X$ 服从标准高斯分布

若 $X$ 服从标准高斯分布，即 $X\sim N(0,1)$，那么 $\sigma X+\mu\sim N(\mu,\sigma^2)$

多元高斯分布是一维高斯分布的推广，为了引入它，需要先了解协方差与协方差矩阵

协方差

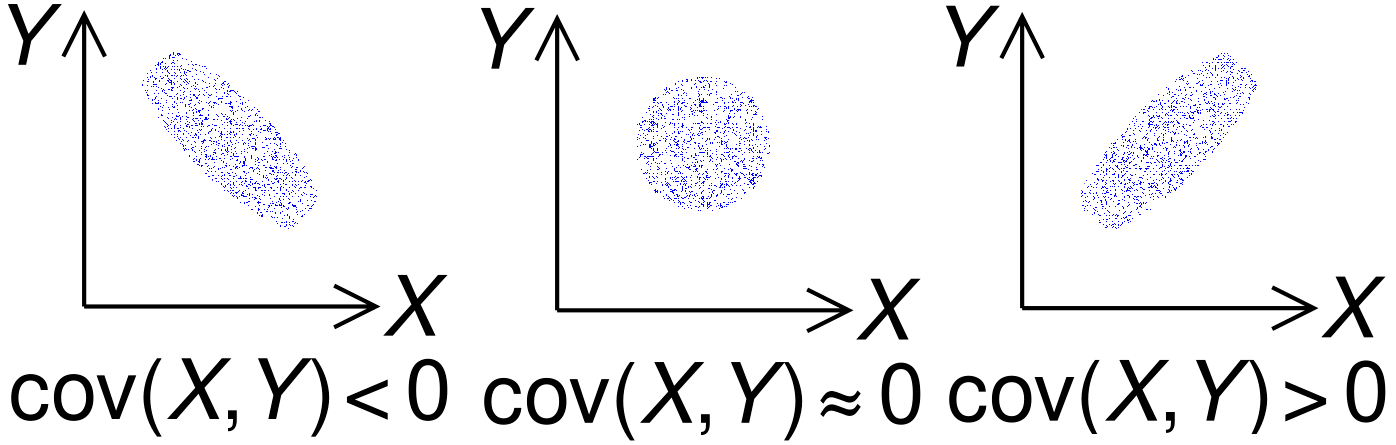
协方差（convariance）用于衡量随机变量间的关联程度

若 $X$ 和 $Y$ 是定义在样本空间 $\Omega$ 上的两个随机变量，它们的期望为 $\mathrm{E}X$ 和 $\mathrm{E}Y$，则协方差定义为：

$$ \mathrm{cov}(X,Y)=\mathrm{E}[(X-\mathrm{E}X)(Y-\mathrm{E}Y)] $$

根据期望的运算律，这个式子也可以写成：

$$ \begin{aligned} \mathrm{cov}(X,Y)&=\mathrm{E}[(X-\mathrm{E}X)(Y-\mathrm{E}Y)]\\ &=\mathrm{E}(XY-X\mathrm{E}Y-Y\mathrm{E}X+\mathrm{E}X\mathrm{E}Y)\\ &=\mathrm{E}(XY)-\mathrm{E}X\mathrm{E}Y-\mathrm{E}X\mathrm{E}Y+\mathrm{E}X\mathrm{E}Y\\ &=\mathrm{E}(XY)-\mathrm{E}X\mathrm{E}Y \end{aligned} $$

对于两个随机变量 $X$ 和 $Y$，协方差有如下性质：

如果两个随机变量相互独立，那么 $\mathrm{cov}(X,Y)=0$
$\mathrm{cov}(X,Y)=\mathrm{cov}(Y,X)$
$\mathrm{cov}(X,X)=\mathrm{var}(X)$，方差

二次型与正定矩阵

对于一个对称矩阵 $\boldsymbol A$ 和一个 $n$ 元列向量 $\boldsymbol x=[x_1,...,x_n]^T$，函数 $f(x_1,x_2,...,x_n)=\boldsymbol x^T\boldsymbol A\boldsymbol x$ 是一个齐次的二次函数，称该函数是二次型

其中，$f$ 展开后是这样的：

$$ \begin{aligned} f(\boldsymbol x)=\boldsymbol x^T\boldsymbol A\boldsymbol x &= \begin{bmatrix}x_1 & \cdots & x_n\end{bmatrix} \begin{bmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{n1} & \cdots & a_{nn} \end{bmatrix} \begin{bmatrix}x_1 \\ \vdots \\ x_n\end{bmatrix} \\ &= \begin{bmatrix}\sum_{i=1}^nx_ia_{i1} & \cdots & \sum_{i=1}^nx_ia_{in}\end{bmatrix} \begin{bmatrix}x_1 \\ \vdots \\ x_n\end{bmatrix} \\ &= \sum_{i=1}^nx_i\sum_{j=1}^nx_ja_{ji} \\ &= \sum_{i,j=1}^na_{ij}x_ix_j \end{aligned} $$

对于一个二次型 $f(\boldsymbol x)$ 和对应的对称矩阵 $\boldsymbol A$，如果：

对于任意 $\boldsymbol x\in\mathbb{R}^n$，都有 $f(\boldsymbol x)\ge 0$，且仅当 $\boldsymbol x=\boldsymbol 0$ 时 $f(\boldsymbol x)=0$，则称 $f$ 为正定二次型，$\boldsymbol A$ 为正定矩阵，记作 $\boldsymbol A>0$
对于任意 $\boldsymbol x\in\mathbb{R}^n$，都有 $f(\boldsymbol x)\ge 0$，且存在 $\boldsymbol x\ne\boldsymbol 0$ 时 $f(\boldsymbol x)=0$，则称 $f$ 为半正定二次型，$\boldsymbol A$ 为半正定矩阵，记作 $\boldsymbol A\ge 0$
负定和半负定类似
存在 $\boldsymbol a\in\mathbb{R}^n$ 使得 $f(\boldsymbol a)>0$ 也存在 $\boldsymbol b\in\mathbb{R}^n$ 使得 $f(\boldsymbol b)<0$ 则称为不定

正定矩阵有如下性质：

所有特征值都是正的
所有顺序主子式都是正的
可逆，且逆矩阵仍正定
如果 $\mathrm A$ 和 $\boldsymbol B$ 正定，任取 $r>0$，$r\boldsymbol A$、$\boldsymbol A+\boldsymbol B$、$\boldsymbol A\boldsymbol B\boldsymbol A$、$\boldsymbol B\boldsymbol A\boldsymbol B$ 都正定

协方差矩阵

推广到 $n$ 维随机变量就是协方差矩阵

对于两个随机变量序列 $X=\{x_i\}_{i=1}^m$ 和 $Y=\{y_i\}_{i=1}^n$，它们的协方差矩阵为：

$$ \mathbf{cov}(X,Y)=[\mathrm{cov}(x_i,y_j)]_{m\times n} $$

根据协方差的定义，我们可以得到：

$$ \mathbf{cov}(X,Y)=[\mathrm{E}[(x_i-\mathrm Ex_i)(y_j-\mathrm Ey_j)]]_{m\times n}=[\mathrm{E}(x_iy_j)-\mathrm Ex_i\mathrm Ey_j]_{m\times n} $$

如果我们把随机变量序列看成列向量，即 $\boldsymbol{X}=[x_1,x_2,...,x_m]^T$，$\boldsymbol{Y}=[y_1,y_2,...,y_n]^T$，那么协方差矩阵就可以写成：

$$ \mathbf{cov}(\boldsymbol X,\boldsymbol Y)=\mathrm E[(\boldsymbol X-\mathrm E\boldsymbol X)(\boldsymbol Y-\mathrm E\boldsymbol Y)^T] $$

其中，对于矩阵 $\boldsymbol P_{m\times n}=[a_{ij}]_{m\times n}$，它的期望定义为：

$$ \mathrm E\boldsymbol P=[\mathrm Ea_{ij}]_{m\times n} $$

此外，一般用 $\boldsymbol \Sigma_{\boldsymbol X}$ 表示 $\mathbf{cov}(\boldsymbol X,\boldsymbol X)$，可以发现，它的对角线上的元素为对应随机变量的方差

$\boldsymbol \Sigma$ 有如下性质：

$\boldsymbol \Sigma$ 是对称的
$\boldsymbol \Sigma$ 是半正定的：
$$ \begin{aligned} \boldsymbol c^T\boldsymbol\Sigma\boldsymbol c &= \sum_{i,j=1}^nc_ic_j\mathrm{cov}(x_i,x_j) \\ &= \sum_{i,j=1}^nc_ic_j\mathrm E[(x_i-\mathrm Ex_i)(x_j-\mathrm Ex_j)] \\ &= \mathrm E\left[\sum_{i,j=1}^nc_i(x_i-\mathrm Ex_i)\cdot c_j(x_j-\mathrm Ex_j)\right] \\ &= \mathrm E\left[\sum_{i=1}^nc_i(x_i-\mathrm Ex_i)\sum_{j=1}^nc_j(x_j-\mathrm Ex_j)\right] \\ &= \mathrm E\left\{\left[\sum_{i=1}^nc_i(x_i-\mathrm Ex_i)\right]^2\right\}\ge 0 \end{aligned} $$
$\boldsymbol \Sigma^{-1}$ 是半正定的

雅可比行列式

有时，找到一个函数 $\boldsymbol T$ 将一个新区域通过它射到目标区域可以更好地求出面积，例如：

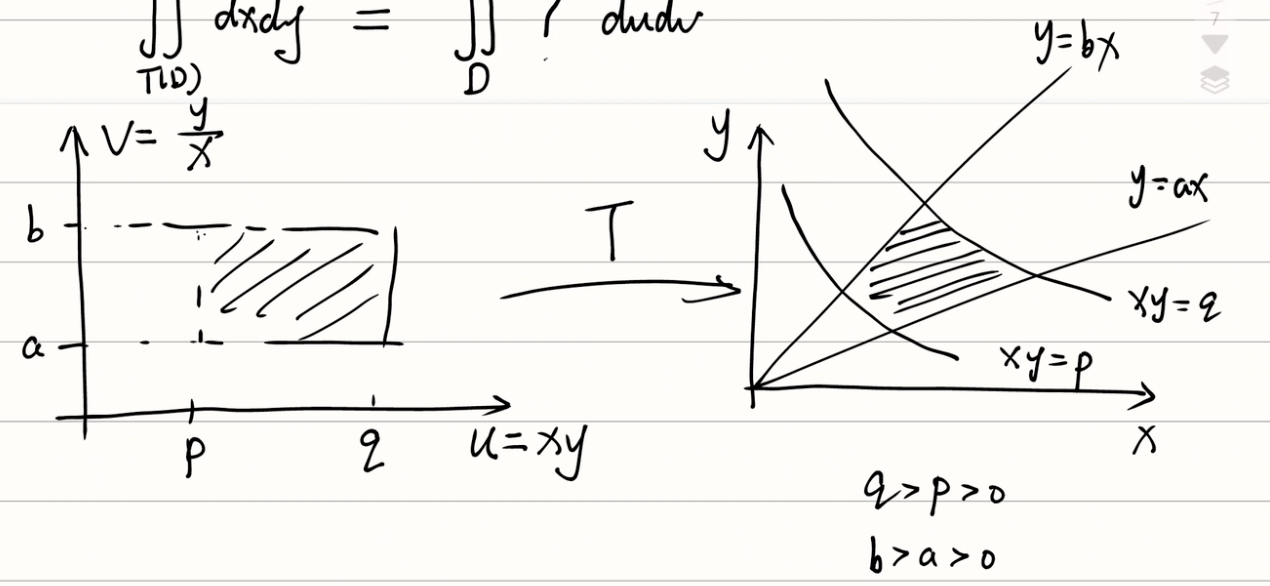
其中，$\boldsymbol T$ 可以表示成：

$$ \begin{equation} \boldsymbol T:\left\{ \begin{aligned} x & = x(u,v) \\ y & = y(u,v) \end{aligned} \right. \end{equation} $$

假设各种东西的性质都足够好，我们要求面积的话需要进行微分，这里就需要二元函数的微分：

$$ \begin{aligned} \mathrm dx=\frac{\partial x}{\partial u}\mathrm du+\frac{\partial x}{\partial v}\mathrm dv\\ \mathrm dy=\frac{\partial y}{\partial u}\mathrm du+\frac{\partial y}{\partial v}\mathrm dv \end{aligned} $$

面积就可以这么求（由于是求面积，所以对积分内部加上绝对值，因为映射到的形状可能有折叠）：

$$ \begin{aligned} \iint_{T(D)} 1\mathrm dx\mathrm dy&=\iint_{D}\left\vert\left(\frac{\partial x}{\partial u}\mathrm du+\frac{\partial x}{\partial v}\mathrm dv\right)\left(\frac{\partial y}{\partial u}\mathrm du+\frac{\partial y}{\partial v}\mathrm dv\right)\right\vert \\ &=\iint_D\left\vert\frac{\partial x}{\partial u}\frac{\partial y}{\partial v}-\frac{\partial x}{\partial v}\frac{\partial y}{\partial u}\right\vert\mathrm du\mathrm dv \end{aligned} $$

其中，因为 $\mathrm d u$ 和 $\mathrm dv$ 相关的乘积叫做楔积，满足：

$\mathrm du\mathrm dv=-\mathrm dv\mathrm du$
$\mathrm du\mathrm du=\mathrm dv\mathrm dv=0$

这样，我们就可以把对于 $(x,y)$ 求面积转换为对 $(u,v)$ 求面积

可以把 $\mathrm dx$ 和 $\mathrm dy$ 的式子写成矩阵形式，那么：

$$ \mathrm d\begin{bmatrix}x \\ y\end{bmatrix} =\begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{bmatrix} \begin{bmatrix}u \\ v\end{bmatrix} $$

中间的二阶方阵就是雅可比矩阵，记作 $\boldsymbol J$，同时，可以发现雅可比矩阵的行列式绝对值与上面的积分结果相同，也就是说上面的面积计算可以写成：

$$ \iint 1\mathrm dx\mathrm dy=\iint \left\Vert\boldsymbol J\right\Vert\mathrm du\mathrm dv $$

我们将其推广一下，可以得到雅可比矩阵的定义

对于函数 $\boldsymbol f:\mathbb R^n\to \mathbb R^m$，即从 $\boldsymbol x\in \mathbb R^n$ 映射到 $\boldsymbol f(\boldsymbol x)\in \mathbb R^m$，雅可比矩阵为：

$$ \boldsymbol J= \begin{bmatrix}\frac{\partial\boldsymbol f}{\partial x_1} & \cdots & \frac{\partial\boldsymbol f}{\partial x_n}\end{bmatrix} =\begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_n} \end{bmatrix} $$

雅可比行列式即 $\left\vert\boldsymbol J\right\vert$，一般把它表示成：

$$ \frac{\partial(f_1,f_2,...,f_m)}{\partial(x_1,x_2,...,x_n)}=\left\vert\begin{matrix} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_n} \end{matrix}\right\vert $$

假设 $m=1$，那么雅可比矩阵就退化成了梯度

通用的换元求积分式子：

$$ \iint_{T(D)}\boldsymbol f(x,y)\mathrm dx\mathrm dy =\iint_{D}\boldsymbol f\left(x(u,v),y(u,v)\right)\left\vert\frac{\partial(x,y)}{\partial(u,v)}\right\vert\mathrm du\mathrm dv $$

概率密度变换公式

设已知随机变量 $X$ 的分布函数为 $F(x)$，概率密度函数为 $f_X(x)$，设 $Y=g(X)$，其中 $g(\cdot)$ 是一个严格单调的函数，且导函数 $g'(\cdot)$ 存在，则 $Y$ 的概率密度函数为：

$$ f_Y(y)=f_X(g^{-1}(y))\left\vert (g^{-1})'(y)\right\vert $$

证：

在递增情况下：

$$ F_Y(y)=P(Y\lt y)=P(g(X)\lt y)=P(X\lt g^{-1}(y))=F_X(g^{-1}(y)) $$

所以：

$$ f_Y(y)=F_Y'(y)=f_X(g^{-1}(y))(g^{-1})'(y) $$

递减情况相似，加个绝对值就能表示这两种情况

再来看多元的情况。设有随机向量 $\boldsymbol Z\in \mathbb R^n$，它的密度为 $f_{\boldsymbol Z}(z)$，定义变换：

$$ \boldsymbol X=T(\boldsymbol Z),\quad T:\mathbb R^n\to\mathbb R^n $$

假设 $T$ 光滑且可逆，那么与一维类似：

$$ F_{\boldsymbol X}(\boldsymbol x)=P(\boldsymbol X\in B_{\boldsymbol x})=P(T(\boldsymbol Z)\in B_{\boldsymbol x})=P(\boldsymbol Z\in T^{-1}(B_{\boldsymbol x}))=F_{\boldsymbol Z}(T^{-1}(\boldsymbol x)) $$

然后再求导：

$$ f_{\boldsymbol X}(\boldsymbol x)=f_{\boldsymbol Z}(T^{-1}(\boldsymbol x))\left\vert\frac{\partial (T^{-1}_1,...,T^{-1}_n)}{\partial(x_1,...,x_n)}\right\vert $$

其中，后一项是雅可比行列式

多元高斯分布

设 $X_1$ 和 $X_2$ 均服从一元标准高斯分布，概率密度函数为：

$$ f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} $$

$X_1$ 和 $X_2$ 相互独立，所以二者的联合概率密度函数就是两个边缘概率密度函数相乘，即：

$$ f(\boldsymbol x)=f(x_1)f(x_2)=\frac{1}{2\pi}e^{-\frac{x_1^2+x_2^2}{2}} $$

推广到 $n$ 个相互独立的服从一元标准高斯分布随机变量 $X_1,X_2,...,X_n$ 后，联合概率密度函数为：

$$ \begin{aligned} f(\boldsymbol x)&=\frac{1}{(2\pi)^{n/2}}e^{-\frac{x_1^2+x_2^2+\cdots+x_n^2}{2}} \\ &=\frac{1}{(2\pi)^{n/2}}e^{-\frac{\boldsymbol x^T\boldsymbol x}{2}} \end{aligned} $$

继续推广到 $n$ 个相互独立的服从高斯分布的随机变量 $Y_1,Y_2,...,Y_n$，它们可以表示成：

$$ Y_i=\sigma_i X_i+\mu_i $$

写成矩阵形式：

$$ \begin{aligned} \boldsymbol Y=\begin{bmatrix} Y_1 \\ \vdots \\ Y_n \end{bmatrix} &=\begin{bmatrix} \sigma_1 & & \\ & \ddots & \\ & & \sigma_n \end{bmatrix}\begin{bmatrix} X_1 \\ \vdots \\ X_n \end{bmatrix}+\begin{bmatrix} \mu_1 \\ \vdots \\ \mu_n \end{bmatrix} \\ &=\boldsymbol A\boldsymbol X+\boldsymbol \mu \\ \end{aligned} $$

设 $T:\mathbb R^n\to\mathbb R^n$：

$$ T(\boldsymbol x)=\boldsymbol A\boldsymbol x+\boldsymbol \mu $$

即：

$$ \boldsymbol Y=T(\boldsymbol X) $$

那么有：

$$ T^{-1}(\boldsymbol x)=\boldsymbol A^{-1}(\boldsymbol x-\boldsymbol \mu) $$

它的雅可比行列式为：

$$ \left\vert\frac{\partial (T^{-1}_1,...,T^{-1}_n)}{\partial(x_1,...,x_n)}\right\vert=\left\vert \boldsymbol A^{-1}\right\vert=\left\vert \boldsymbol A\right\vert^{-1} $$

根据概率密度变换公式，可以得到：

$$ \begin{aligned} f_{\boldsymbol Y}(\boldsymbol y)&=f_{\boldsymbol X}(T^{-1}(\boldsymbol y))\left\vert\frac{\partial (T^{-1}_1,...,T^{-1}_n)}{\partial(y_1,...,y_n)}\right\vert \\ &=\frac{1}{(2\pi)^{n/2}}e^{-\frac{1}{2}\left[\boldsymbol A^{-1}(\boldsymbol y-\boldsymbol \mu)\right]^T\left[\boldsymbol A^{-1}(\boldsymbol y-\boldsymbol \mu)\right]}\left\vert \boldsymbol A\right\vert^{-1} \\ &=\frac{1}{(2\pi)^{n/2}}e^{-\frac{1}{2}(\boldsymbol y-\boldsymbol \mu)^T(\boldsymbol A^{-1})^T\boldsymbol A^{-1}(\boldsymbol y-\boldsymbol \mu)}\left\vert \boldsymbol A\right\vert^{-1} \\ &=\frac{1}{(2\pi)^{n/2}\vert\boldsymbol\Sigma\vert^{1/2}}e^{-\frac{1}{2}(\boldsymbol y-\boldsymbol \mu)^T\boldsymbol \Sigma^{-1}(\boldsymbol y-\boldsymbol \mu)} \end{aligned} $$

当 $Y_1,Y_2,...,Y_n$ 并不互相独立时，上面的 $\boldsymbol A$ 就不是一个对角矩阵了，它就变成了一个更一般的实矩阵，但仍然满足：

$$ \boldsymbol Y=\boldsymbol A\boldsymbol X+\boldsymbol \mu $$

即通过线性变换引入相关性，这样不会破坏其线性封闭性

此时，我们发现：

$$ \begin{aligned} \boldsymbol\Sigma&=\mathrm E[(\boldsymbol Y-\mathrm E\boldsymbol Y)(\boldsymbol Y-\mathrm E\boldsymbol Y)^T] \\ &=\mathrm E[(\boldsymbol Y-\boldsymbol \mu)(\boldsymbol Y-\boldsymbol \mu)^T] \\ &=\mathrm E[(\boldsymbol A\boldsymbol X)(\boldsymbol A\boldsymbol X)^T] \\ &=\boldsymbol A\mathrm E[\boldsymbol X\boldsymbol X^T]\boldsymbol A^T \\ &=\boldsymbol A\boldsymbol A^T \end{aligned} $$

由行列式相关的恒等式 $\vert \boldsymbol A\boldsymbol B\vert=\vert \boldsymbol A\vert\vert\boldsymbol B\vert$ 可以得到：

$$ \vert \boldsymbol A\vert=\vert\boldsymbol\Sigma\vert^{1/2} $$

所以推广到一般情况下仍然满足上面的概率密度函数

对于服从 $n$ 元高斯分布的向量 $\boldsymbol X$，它的概率密度函数为：

$$ \boxed{f(\boldsymbol x)=\frac{1}{(2\pi)^{n/2}\vert\boldsymbol\Sigma\vert^{1/2}}e^{-\frac{1}{2}(\boldsymbol x-\boldsymbol \mu)^T\boldsymbol \Sigma^{-1}(\boldsymbol x-\boldsymbol \mu)}} $$

其中 $\boldsymbol \Sigma$ 表示协方差矩阵，$\boldsymbol \mu$ 表示期望，它只由这两个参数控制

高斯椭球

三维高斯分布在空间中可以可视化成一个“椭球”，$\boldsymbol \mu$ 影响了椭球的中心点位置，$\boldsymbol \Sigma$ 影响了椭球的形状

上面提到，协方差矩阵及其逆矩阵是半正定的，所以如果我们拿概率密度函数的指数部分来看，可以简化为这样一个式子：

$$ (\boldsymbol x-\boldsymbol \mu)^T\boldsymbol \Sigma^{-1}(\boldsymbol x-\boldsymbol \mu)=c^2 $$

如果我们固定常数 $c$，那么就形成了一个椭球面

协方差矩阵的正交对角化

参考 https://zhuanlan.zhihu.com/p/9846909742，有如下结论：

实对称矩阵的特征值一定是实数
实对称矩阵的不同特征值对应的特征向量正交

所以：实对称矩阵可以正交对角化

协方差矩阵的逆矩阵是对称且半正定的，所以它也可以正交对角化，即可以分解成：

$$ \boldsymbol \Sigma=\begin{bmatrix}\boldsymbol\alpha & \boldsymbol\beta & \boldsymbol\gamma\end{bmatrix} \begin{bmatrix} \lambda_1 & 0 & 0 \\ 0 & \lambda_2 & 0 \\ 0 & 0 & \lambda_3 \end{bmatrix} \begin{bmatrix} \boldsymbol\alpha^T \\ \boldsymbol\beta^T \\ \boldsymbol\gamma^T \end{bmatrix}=\boldsymbol Q\boldsymbol \Lambda\boldsymbol Q^T $$

并且有：

$$ \boldsymbol Q\boldsymbol Q^T=\boldsymbol Q^T\boldsymbol Q=\boldsymbol I $$

那么：

$$ \boldsymbol \Sigma^{-1}=\boldsymbol Q\boldsymbol \Lambda^{-1}\boldsymbol Q^T $$

假设 $\boldsymbol\mu =\boldsymbol 0$，我们代入看一下：

$$ \begin{aligned} \boldsymbol x^T\boldsymbol \Sigma^{-1}\boldsymbol x&= \boldsymbol x^T \begin{bmatrix}\boldsymbol\alpha & \boldsymbol\beta & \boldsymbol\gamma\end{bmatrix} \begin{bmatrix} 1/\lambda_1 & 0 & 0 \\ 0 & 1/\lambda_2 & 0 \\ 0 & 0 & 1/\lambda_3 \end{bmatrix} \begin{bmatrix} \boldsymbol\alpha^T \\ \boldsymbol\beta^T \\ \boldsymbol\gamma^T \end{bmatrix} \boldsymbol x \\ &=\boldsymbol x^T\left(\frac{\boldsymbol\alpha\boldsymbol\alpha^T}{\lambda_1}+\frac{\boldsymbol\beta\boldsymbol\beta^T}{\lambda_2}+\frac{\boldsymbol\gamma\boldsymbol\gamma^T}{\lambda_3}\right)\boldsymbol x \\ &=\frac{(\boldsymbol x^T\boldsymbol\alpha)(\boldsymbol\alpha^T\boldsymbol x)}{\lambda_1}+\frac{(\boldsymbol x^T\boldsymbol\beta)(\boldsymbol\beta^T\boldsymbol x)}{\lambda_2}+\frac{(\boldsymbol x^T\boldsymbol\gamma)(\boldsymbol\gamma^T\boldsymbol x)}{\lambda_3} \\ &=\frac{(\boldsymbol\alpha^T\boldsymbol x)^2}{\lambda_1}+\frac{(\boldsymbol\beta^T\boldsymbol x)^2}{\lambda_2}+\frac{(\boldsymbol\gamma^T\boldsymbol x)^2}{\lambda_3} \end{aligned} $$

可以看到，本质上它将 $\boldsymbol x$ 投影到新的坐标系 $(\boldsymbol\alpha,\boldsymbol\beta,\boldsymbol\gamma)$ 上，按各自的伸缩系数 $1/\lambda_1$、$1/\lambda_2$、$1/\lambda_3$ 加权求平方和

几何上，它刻画了椭球的形状和方向

正交对角化的另一种形式

由于协方差矩阵 $\boldsymbol \Sigma$ 是半正定的，前面提到半正定矩阵的特征值一定是非负的，所以中间的 $\boldsymbol\Lambda$ 可以“开根号”，所以可以分解成：

$$ \boldsymbol \Sigma=\boldsymbol R\boldsymbol S\boldsymbol S^T\boldsymbol R^T $$

其中 $\boldsymbol R$ 表示旋转，它负责旋转到新的坐标系，$\boldsymbol S$ 表示缩放，表示在新的坐标系下各个坐标轴的缩放