连续函数不能在计算机中直接表示
函数的采样（samples）：存储函数不同点的值，并且在需要的时候重建（reconstruct）它们之间的值
函数在一个或多个维度上的栅格（lattice）点上进行采样，并且我们需要从样本数组中重建原始的连续函数
锯齿（aliasing，走样）
数字音频：一维采样
模数转换器（analog-to-digital converter，A/D converter，或 ADC）
数模转换器（digital-to-analog converter，D/A converter，或 DAC）
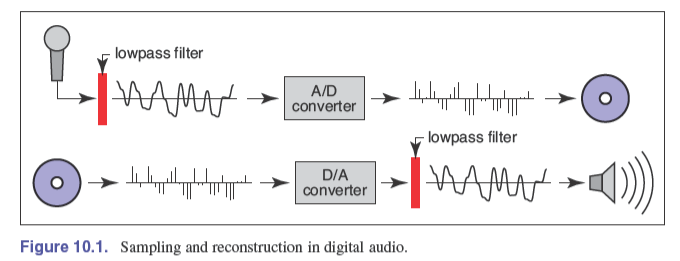
两个问题：
- 良好的每秒采样数取决于声音的高频程度，如果不够则会产生奇怪的声音，为了避免这些欠采样伪像（undersampling artifacts），数字录音机对 ADC 的输入进行过滤（filter），以去除可能导致问题的高频。
- DAC 会产生阶梯状的图像，这些阶梯的作用类似于噪声，增加了高频的、依赖于信号的嗡嗡声。为了消除这种重建伪像（reconstruction artifact），数字音频播放器对 DAC 的输出进行过滤，以剔除波形。
采样伪影（Sampling Artifacts）与走样（Aliasing）
欠采样和重建伪影也发生在图形中的其他采样信号中，解决方案是相同的：在采样之前进行滤波，并在重建期间再次过滤
走样（aliasing）：由于收集时采样率不足，导致重建后的数据看起来很诡异
在图像中，走样（锯齿）通常是摩尔纹图案（moire patterns）的形式，这些图案是样本网格与图像中的常规特征相互作用的结果。
合成图像中的另一个例子是渲染直线时的“台阶”
采样和重建的基本问题可以简单地理解为特征太小或太大，但一些更定量的问题更难回答：
- 采样率要高到多少才能保证好的结果？
- 什么类型的滤波器适合采样和重建？
- 需要多大程度的平滑来避免走样？
卷积（Convolution）
卷积是一种函数运算：它需要两个函数并将它们组合起来以产生一个新函数
卷积是一个简单的数学概念，是采样、过滤和重建算法的基础
卷积既可以应用于连续函数，也可以应用于离散序列，它还可以应用于在一维、二维或更高维域上定义的函数
为了定义方便，我们一般假设函数的定义域永远延伸
离散卷积（Discrete Convolution）
$$ (a*b)[i]=\sum_ja[j]b[i - j] $$性质：满足交换律、结合律和分配率
$$ (a*b)[i]=(b*a)[i]\\ (a*(b*c))[i]=((a*b)*c)[i]\\ (a*(b+c))[i]=(a*b+a*c)[i] $$$b$ 向右移位 $j$ 位之后表示成 $b_{\rightarrow j}$，有：
$$ b_{\rightarrow j}[i]=b[i-j] $$这叫做移位滤波器（Shifted Filters），我们改一下前面的定义：
$$ (a*b)[i]=\sum_ja[j]b[i - j]=\sum_ja[j]b_{\rightarrow j}[i] $$所以，卷积可以看成是移位滤波器的（加权）和：
$$ (a*b)=\sum_ja[j]b_{\rightarrow j} $$特殊的函数：
单位函数 $d[i]=\dots,0,0,1,0,0,\dots$（仅在 $i=0$ 时为 $1$），被称为离散脉冲（discrete impulse），有：
$$ (a*d)[i]=a[i] $$阶跃函数（step function），好像也可以叫做 box function？：
$$ b[i]=\frac{1}{2r+1}\begin{cases}1 & -r\le i\le r\\0&\text{Otherwise}\end{cases} $$
连续函数的卷积
$$ (f*g)(x)=\int_{-\infty}^{+\infty}f(t)g(x-t)\mathrm dt $$性质仍然满足交换律、结合律和分配率，也可以写成移位滤波器的加权和：
$$ (f*g)=(g*f)\\ (f*(g*h))=((f*g)*h)\\ (f*(g+h))=(f*g+f*h)\\ (f*g)=\int_{-\infty}^{+\infty}f(t)g_{\rightarrow t}\mathrm dt $$特殊的函数：
帐篷函数（tent function）：两个 box function 卷积：
$$ f(x)=\begin{cases}1 & -\frac{1}{2}\le x\le \frac{1}{2}\\0&\text{Otherwise}\end{cases} $$卷积后：
$$ \begin{align} (f*f)(x)&=\int_{-\infty}^{+\infty}f(t)f(x-t)\mathrm dt\\ &=\begin{cases}1- |x| & -1\le x\le 1\\0&\text{Otherwise}\end{cases} \end{align} $$这个函数被叫做帐篷函数
狄拉克 delta 函數（Dirac delta function）或狄拉克脉冲函数（Dirac impulse function）：
$$ \delta(x)=\begin{cases}+\infty & x=0\\0&x\ne 0\end{cases} $$这个类似离散卷积的单位函数，与 $f(x)$ 卷积后得到它本身：
$$ (\delta *f)(x)=\int_{-\infty}^{+\infty}\delta(t)f(x-t)\mathrm dt=f(x) $$
离散-连续函数卷积
两种方法连接离散和连续这两个世界：
一种是采样（连续到离散），可以简单地采样如下：
$$ a[i]=f(i) $$另一种是重建（离散到连续），使用离散函数与连续函数的卷积形式：
$$ (a*f)(x)=\sum_ia[i]f(x-i) $$注意这里不能交换 $a$ 与 $f$
可以写成移位滤波器的加权和：
$$ (a*f)=\sum_ia[i]f_{\rightarrow i} $$与样条（spline）密切相关
高维卷积
$$ (a*b)[i,j]=\sum_{i'}\sum_{j'}a[i',j']b[i-i',j-j']\\ (f*g)(x,y)=\int\int f(x',y')g(x-x',y-y')\mathrm dx'\mathrm dy'\\ (a*f)(x,y)=\sum_i\sum_ja[i,j]f(x-i,y-j) $$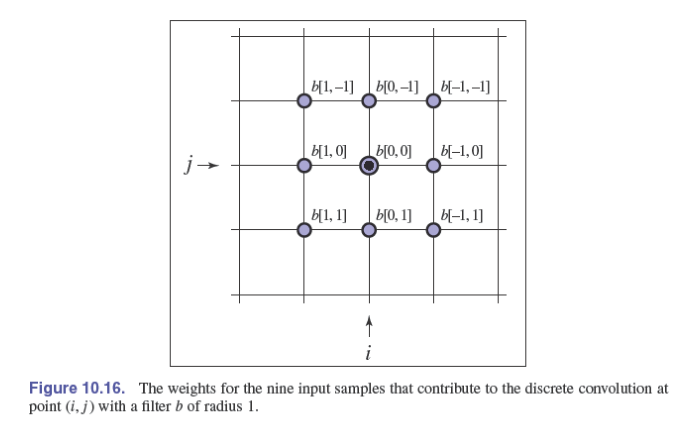
卷积滤波器（Convolution Filters）
常见滤波器：
盒子滤波（box filter），半径为 $r$：
$$ a_{\text{box},r}[i]=\begin{cases}1/(2r+1) & |i|\le r\\0&\text{Otherwise}\end{cases}\\ f_{\text{box},r}(x)=\begin{cases}1/2r & -r\le x\lt r\\0&\text{Otherwise}\end{cases}\\ $$帐篷滤波（tent filter）：
$$ f_\text{tent}=\begin{cases}1- |x| & |x|\lt 1\\0&\text{Otherwise}\end{cases} $$高斯滤波（Gaussian filter）：
$$ f_{\text{G},\sigma}(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-x^2/2\sigma^2} $$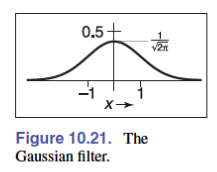
它的范围是无穷，但是可以裁剪，变成 trimmed Gaussian，一般有一个参数 $s$，半径是 $s\sigma$
B-Spline Cubic Filter：是由分段三阶多项式构成的一个特殊函数，拥有连续的一阶微分和二阶微分，通常的半径为 $2$，值得注意的是它可以写作四个 box filter 的卷积形式
$$ f_\text{B}(x)=\frac{1}{6}\begin{cases}-3(1-|x|)^3+3(1-|x|)^2+3(1-|x|)+1 & -1\le x\lt 1\\ (2-|x|)^3&1\le |x|\le 2\\ 0&\text{Otherwise}\end{cases} $$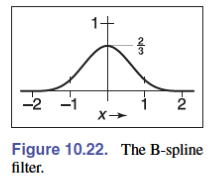
Catmull-Rom Cubic Filter：是上个的修改版，其顶端到 $1$，但是在 $[1,2]$ 之间存在一些负数部分
$$ f_\text{C}(x)=\frac{1}{2}\begin{cases}-3(1-|x|)^3+4(1-|x|)^2+(1-|x|) & -1\le x\lt 1\\ (2-|x|)^3-(2-|x|)^2&1\le |x|\le 2\\ 0&\text{Otherwise}\end{cases} $$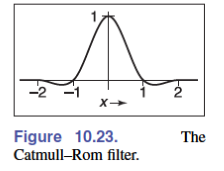
Mitchell-Netravali Cubic Filter：结合了上两个 filter，分别的权重为 $1/3$ 和 $2/3$
$$ f_\text{M}(x)=\frac{1}{3}f_\text{B}(x)+\frac{2}{3}f_\text{C}(x) $$
一些术语：
脉冲响应（impulse response）：函数在单位 $1$ 的脉冲（impulse）下产生的效果
插值（interpolating）
振铃（ringing）或过冲（overshoot）：在被过滤函数值的急剧变化处产生额外的振荡（oscillation）
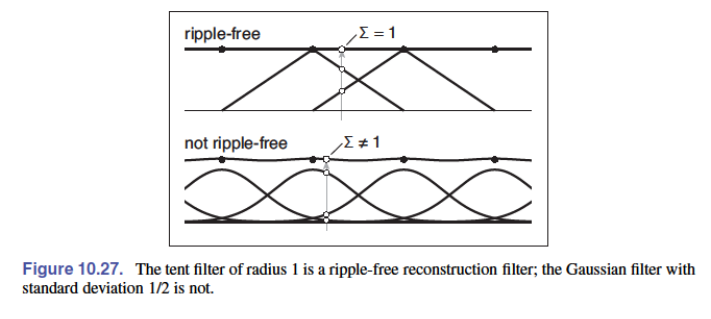
ripple free：把一个常数序列映射成常数函数的滤波器，等价于：
$$ \sum_if(x+i)=1 $$可以去波纹，只需要（不懂这个怎么实现）：
$$ (\overline {a*f})(x) =\frac{\sum_i a[i]f(x − i)}{\sum_i a[i]} $$连续度（degree of continuity）：$C^0$ 表示连续但一阶导不连续，$C^1$、$C^2$ 以此类推
可分离滤波器（Separable Filters）：
可以分成两个函数的乘积
$$ f_2(x,y)=f_1(x)f_1(y)\\ b_2[i, j] = b_1[i]b_1[j] $$例子有可分离帐篷滤波器（separable tent filter）、二维高斯滤波器（2D Gaussian filter）
可分离过滤器可以简化计算，如：
$$ \begin{align} (a*b_2)[i,j]&=\sum_{i'}\sum_{j'}a[i',j']b_2[i-i',j-j']\\ &=\sum_{i'}\sum_{j'}a[i',j']b_1[i-i']b_1[j-j']\\ &=\sum_{i'}b_1[i-i']\sum_{j'}a[i',j']b_1[j-j']\\ &\equiv\sum_{i'}b_1[i-i']S[i'] \end{align} $$我们可以先计算 $S[i']$ 并存下来，之后再计算 $(S*b_1)$
图像信号处理
使用离散滤波器进行图像滤波
使用低通滤波器进行图像模糊，高斯滤波器应用最广泛
与模糊相对的是锐化，一种方法是使用反锐化蒙版（unsharp mask）：从原始图像中减去一张模糊图像的 $\alpha$ 倍，并且重新缩放来避免改变图像的亮度，式子如下：
$$ \begin{align} I_\text{sharp}&=(1+\alpha)I-\alpha(I*f_{g,\sigma})\\ &=I*((1+\alpha)d-\alpha f_{g,\sigma})\\ &=I*f_\text{sharp}(\sigma,\alpha) \end{align} $$其中，$f_{g,\sigma}$ 是标准差为 $\sigma$ 的高斯模糊
另一个组合两个离散滤波器的例子是阴影，通常对原图像的轮廓先移动并模糊，然后再叠加原图像得到阴影
$$ d_{m,n}(i,j)=\begin{cases}1&i=m\text { and }j=n\\0&\text{Otherwise}\end{cases} $$$$ \begin{align} I_\text{shadow}&=(I*d_{m,n})*f_{g,\sigma}\\ &=I*(d_{m,n}*f_{g,\sigma})\\ &=I*f_\text{shadow}(m,n,\sigma) \end{align} $$上面的 $d_{m,n}$ 表示原图像的平移
图像采样中的走样
走样伪影分为两种：摩尔纹（在重复出现相似图像时出现）和锯齿（在锋利部分出现），
这里的问题是图像包含了太多的小尺度特征（small-scale features），我们需要在采样之前，使用滤波器让它变得更加平滑
前面说了几个简单的滤波器，如盒子滤波器（有效，但不如高斯滤波器）、高斯滤波器（对摩尔纹改善更有效，但是会更模糊）等。锐度和摩尔纹之间需要权衡
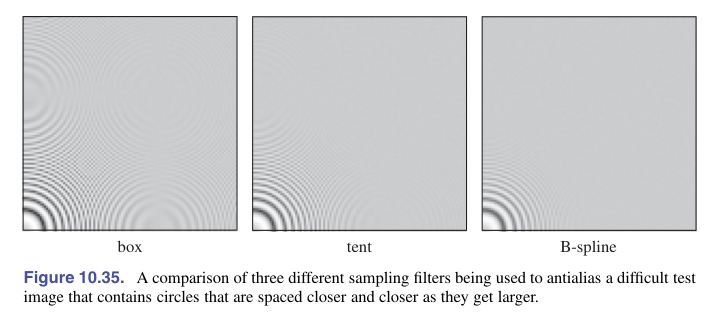
重建与重采样
改变图像大小可以被视为重采样（resampling）操作：首先，从输入样本中重建连续函数，对这个连续函数进行采样
最简单的就是像素丢弃算法（pixel-dropping algorithm），取最近的样本值并输出，这就相当于一像素大小的 box filter
为了避免走样，我们最好再使用一个采样滤波器 $g$ 来卷上刚才的函数，即 $(a*f)*g=a*(f*g)$，这种将采样滤波器和重建滤波器结合的滤波器叫做重采样滤波器（resampling filter）
在重采样时，我们常常以源图像为单位指定一个源矩形（source rectangle），表示我们希望保留在新的图像的部分。例如，如果我们沿用第三章的设定，我们希望从大小为 $(-0.5,n_x^\text{old}-0.5)\times(-0.5,n_y^\text{old}-0.5)$ 的源图像选择一部分（源矩形） $(x_l,x_h)\times(y_l,y_h)$ 重采样成大小为 $(-0.5,n_x^\text{new}-0.5)\times(-0.5,n_y^\text{new}-0.5)$ 大小的新图像，那么在新图像的单位下，源矩形中的像素间隔是 $\Delta x=(x_h-x_l)/n_x^\text{new}$、$\Delta y=(y_h-y_l)/n_y^\text{new}$。
一维重采样的伪代码：
function resample(sequence a, float xl, float xh, int n, filter f)
create sequence b of length n
r = f.radius
x0 = xl + dx / 2
for i = 0 to n - 1 do
s = 0
x = x0 + i * dx
for j = ceil(x - r) to floor(x + r) do
s = s + a[i] * f(x - j)
b[i] = s
return b
有一个问题，就是边界部分该怎么处理，有三种：
- 在出界后停止，相当于填充 $0$。会导致亮度降低
- 将下标 bound，如当访问 $a[-10]$ 时返回 $a[0]$。容易实现
- 接近边界时修改滤波器，让它不会超出边界。效果最好，最简单的方法是重新规范化（renormalize），将滤波器除以边界内部分的总和，让边界内的权重之和变成 $1$。为了提高性能，最好将需要重新规范化的与不需要的分开处理
重采样滤波器的选择很重要。有两个独立的问题：过滤器的形状和大小（半径）。对于重建滤波器，我们希望滤波器足够平滑且无波纹；对于采样滤波器，我们希望滤波器足够大以避免欠采样，并且足够平滑来防止摩尔纹
通常，我们会选择一个滤波器形状，并根据输入和输出的相对分辨率对其进行缩放。两个分辨率中较低的一个决定了滤波器的大小。当输出比输入采样更粗略（下采样，缩小图像）时，采样所需的平滑大于重建所需的平滑，因此我们根据输出样本间距来调整滤波器的大小（radius 3）。另一方面，当输出比输入采样更精细（上采样，放大图像）时，重建所需的平滑占主导地位，因此滤波器的大小由输入采样间隔决定（radius 1）。
搞不懂，很抽象
选择过滤器本身是速度和质量之间的权衡。
box filter 最快，tent filter 质量中等，分段的 cubic 质量最好
在分段的 cubic 中，通过在 $f_B$ 和 $f_C$ 之间插值，可以调整平滑度，Mitchell-Netravali Cubic Filter 是一个不错的选择
可分离的滤波器可以速度会更快
采样定理（Sampling Theory）
傅里叶变换（The Fourier Transform）
通过利用所有频率的正弦波相加来表示任何函数
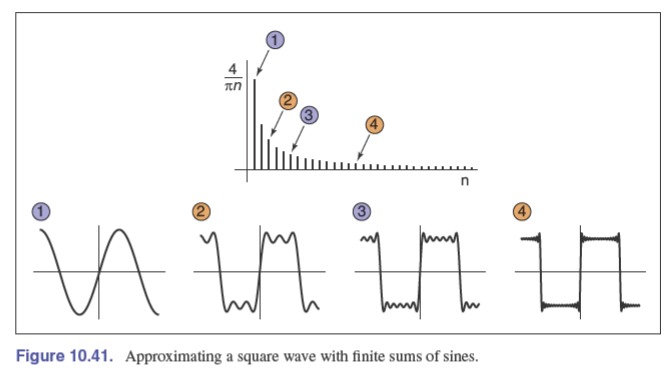
见 傅里叶变换。
傅里叶变换的一些性质：
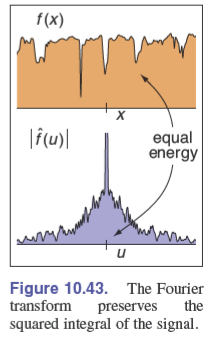
函数和它的傅里叶变换有相同的平方积分：
$$ \int [f(x)]^2\mathrm dx=\int[\mathcal{F}(f)(t)]^2\mathrm dt $$在物理上，表现为他们有相同的能量：
若 $a$ 为常数，有：
$$ \mathcal{F}(af)=a\mathcal{F}(f) $$若 $b$ 为非零常数，有：
$$ \mathcal{F}(f)(x/b)=b\mathcal{F}(f)(bx) $$函数 $f$ 的平均值等于 $\mathcal{F}(f)(0)$
如果 $f$ 是实函数，那么 $\mathcal{F}(f)$ 是偶函数。如果 $f$ 是偶函数，那么 $\mathcal{F}(f)$ 是实函数。
傅里叶变换可以将卷积变为函数的乘积：
$$ \mathcal{F}(f*g)=\mathcal{F}(f)\mathcal{F}(g) $$也可以将乘积变为卷积：
$$ \mathcal{F}(f)*\mathcal{F}(g)=\mathcal{F}(fg) $$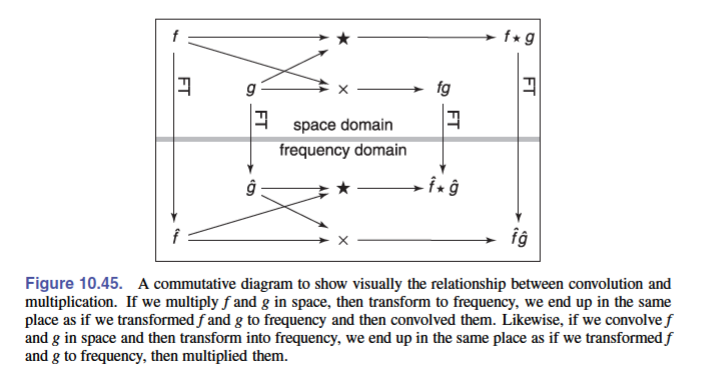
一些傅里叶变换
$$ \mathcal{F}(f_\text{box})=\frac{\sin\pi u}{\pi u}\\ \mathcal{F}(f_\text{tent})=\frac{\sin^2\pi u}{(\pi u)^2}\\ \mathcal{F}(f_\text{B})=\frac{\sin^4\pi u}{(\pi u)^4}\\ \mathcal{F}(f_{\text{G},\sigma=1})=e^{-(2\pi u)^2/2} $$采样定理中的狄拉克脉冲（Dirac Impulses）
通过脉冲来描述样本，例如在 $x=a$ 处如果值是 $f(a)$，那么可以表示为：
$$ f(a)\delta(x-a) $$在一系列等距点上采样一个函数可以表示为将函数乘以一系列等距脉冲之和，称为脉冲串（impulse train），例如，如果我们的间距是 $T$，那么脉冲串为：
$$ s_T(x)=\sum_{i=-\infty}^{+\infty}\delta(x-Ti) $$性质有（理解不了一点）：
$$ \mathcal{F}(s_T)=s_{1/T} $$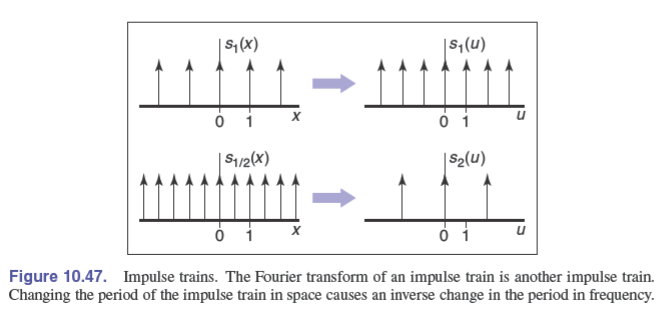
采样、重建与走样（混叠）
介绍了傅里叶变换和狄拉克脉冲后，从频域的角度理解采样和重建过程。
采样就是函数乘上狄拉克脉冲，也就是：
$$ fs_T $$当我们进行傅里叶变换后：
$$ \mathcal{F}(fs_T)=\mathcal{F}(f)*\mathcal{F}(s_T)=\mathcal{F}(f)*s_{1/T} $$也就是：
$$ \mathcal{F}(fs_T)(x)=\sum_{i=-\infty}^{+\infty}\mathcal{F}(f)(x-\frac{i}{T}) $$我们发现，采样在频域上表现为源函数的平移副本的叠加，这就是走样的另一个翻译“混叠”的来源
原始的频谱（spectrum）称为基频谱（base spectrum），平移副本称为混叠频谱（alias spectrum）
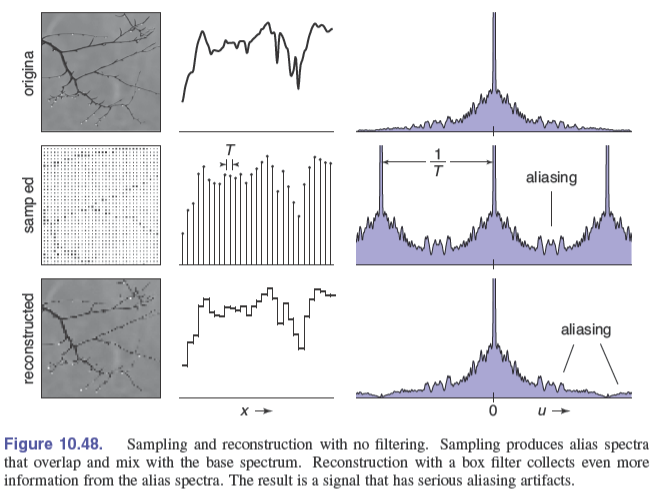
很自然地，我们可以增加采样频率 $T$ 来减少混叠的部分，那么下面的奎斯特准则（Nyquist criterion）就好理解了
频谱的宽度必须小于两个副本之间的距离，即信号中存在的最高频率必须小于采样频率的一半，这被称为奎斯特准则（Nyquist criterion）
允许的最高频率被称为奈奎斯特频率（Nyquist frequency）或奈奎斯特极限（Nyquist limit）
奈奎斯特-香农采样定理（Nyquist-Shannon sampling theorem）指出，原则上，频率不超过奈奎斯特极限的信号可以从样本中准确地重建
回忆一下前面的重建，我们在采样基础上卷上重建滤波器，例如我们卷上 box filter：
$$ (fs_T)*f_\text{box} $$根据傅里叶变换的性质，我们将其变换到频域：
$$ \mathcal{F}((fs_T)*f_\text{box})=\mathcal{F}(fs_T)\mathcal{F}(f_\text{box}) $$代入后得到：
$$ \mathcal{F}((fs_T)*f_\text{box})(x)=\sum_{i=-\infty}^{+\infty}\mathcal{F}(f)(x-\frac{i}{T})\frac{\sin\pi x}{\pi x} $$我们发现，重建在频域上表现为缩放，这里乘上了一个小于等于 $1$ 的参数，我们这种称为低通滤波器
相对于 box filter，有更低的滤波器，表现为在 $x$ 轴上范围的缩小
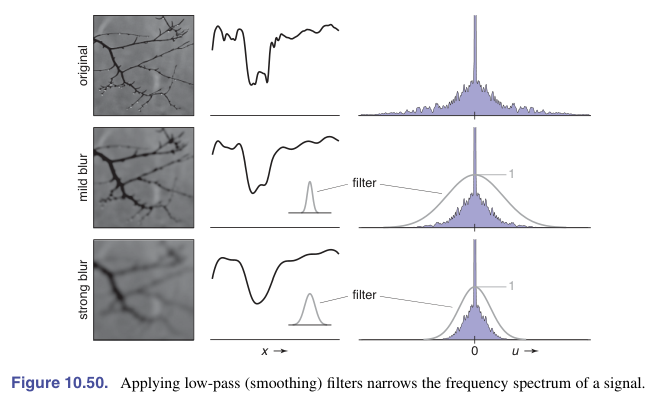
对于一个特定的信号有足够高的采样率，我们不需要使用采样滤波器。但是如果采样率不够，那么我们要进行带宽限制，即使用低通滤波器
剩下的就不看了，看得脑袋疼
真是非常神奇，居然变换到频域之后就这么简单好理解