不改变形状，但是表面的属性值根据位置不同有差异

纹理映射（texture mapping）：用一张叫做纹理图（texture map）、纹理图像（texture image）或者纹理（texture）的图片来存储表面上的细节，然后用数学方法将其映射到表面上

纹理还可以被用来制作阴影和反射、提供照明，甚至定义表面形状

纹理思想很简单，但是有些问题需要解决：

• 纹理很容易被扭曲，设计将纹理映射到表面的功能是具有挑战性的
• 纹理是一个重采样（resampling）过程，重采样可以很容易地引入走样伪影。纹理映射和动画一起使用很容易产生真正戏剧性的走样，并且纹理映射系统的许多复杂性是由这些抗走样（antialiasing）措施带来的。

查找纹理值

纹理查找（texture lookup）：在纹理图像的坐标系统中找出与着色点对应的位置，并在图像中取出该点的颜色，从而得到纹理样本（texture sample）

首先，我们需要一个从表面 $S$ 映射到纹理域 $T$ 的函数 $\phi$，这个函数叫做纹理坐标函数（texture coordinate function）：

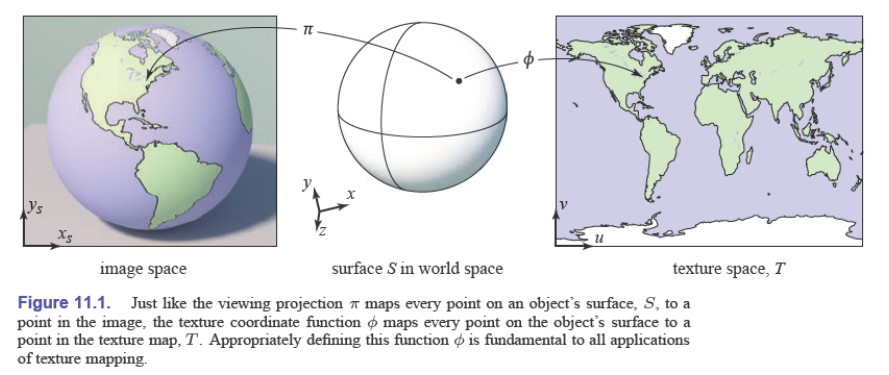
$T$ 常常被称作纹理空间（texture space），通常是一个存储着图像的矩形，常常使用单位正方形 $(u,v)\in[0,1]^2$

虽然是纹理贴到表面上，但 $\phi$ 是一个从表面到纹理的映射

有一个问题：从一个非常倾斜的角度渲染一个高对比度纹理时，会产生走样

现在，有两个主要的议题：

• 定义纹理坐标函数
• 在避免太多走样的情况下查找纹理值

纹理坐标函数

设计纹理坐标函数非常重要，有时表面就是平面，有时是不规则的几何体

并不是图形学专属，制图师在制作地球仪等时也面临相似的问题

设计纹理坐标图是一个平衡相互冲突的关注点的微妙的任务

对于纹理坐标函数 $\phi$ 来说，有几个重要的关注点：

• 双射性（Bijectivity）：确保表面上的每个点映射到纹理空间中的不同点。如果几个点映射到相同的纹理空间点，则纹理中一个点的值将影响表面上的几个点。除非故意地重复（例如具有重复图案的墙纸或地毯）
• 尺寸失真（Size distortion）：纹理的尺度应该在整个表面上近似恒定。也就是说，表面上任何距离相同的近距离点都应该映射到纹理中距离相同的点。对于 $\phi$ 来说，$\phi$ 的导数的大小不应该变化太大。
• 形状扭曲（Shape distortion）：纹理不应该严重扭曲。也就是说，在表面上绘制的小圆圈应映射到纹理空间中的合理圆形，而不是极度挤压或拉长的形状。就 $\phi$ 来说，$\phi$ 的导数在不同方向上不应有太大差异。
• 连续性（Continuity）：不应有太多缝隙，表面上的相邻点应映射到纹理中的相邻点。也就是说，$\phi$ 应该是连续的或具有尽可能少的不连续性。

由参数方程（有 $u$ 和 $v$ 的那个）定义的表面只需取逆就能得到纹理坐标函数，但可能并不具有理想的属性

对于隐式定义或者由三角形网格（应该是一系列三角形）定义的表面，需要其他的方法来定义纹理坐标

定义纹理坐标的两种方式：

• 从表面的空间坐标以几何的方式计算
• 对于三角形网格，将纹理坐标值存储在顶点上并进行插值

以几何方式确定的纹理坐标

用于简单形状或特殊情况

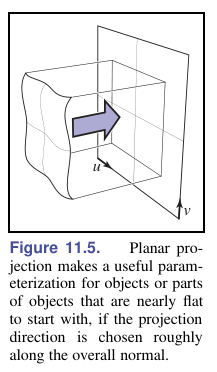
平面投影

最简单的就是平行投影：

其中，$\mathbf M_t$ 表示仿射变换，$*$ 表示我们不关心第三维坐标的值

这对于大多数平坦的表面来说非常有效，表面法线没有太多变化，并且可以通过取平均法线找到一个好的投影方向。

对于封闭形状，平面投影都不是双射的

将 $\mathbf M_t$ 替换为 $\mathbf P_t$ 就能得透视纹理坐标（projective texture coordinate）：

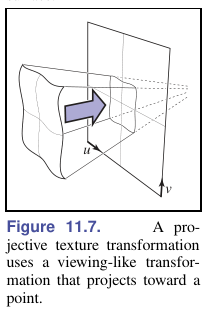
球面坐标

对于球面，经纬度参数化（latitude/longitude parameterization）是一种常用的方法

经纬度参数化在两极附近有很多失真，这可能会导致一些问题，但它确实覆盖了整个球体，仅在一个经线（本初子午线）上会有不连续的情况。

球坐标是 $(r,\theta,\varphi)$，其中取值范围是 $\theta\in[0,\pi]$，$\varphi\in[0,2\pi]$

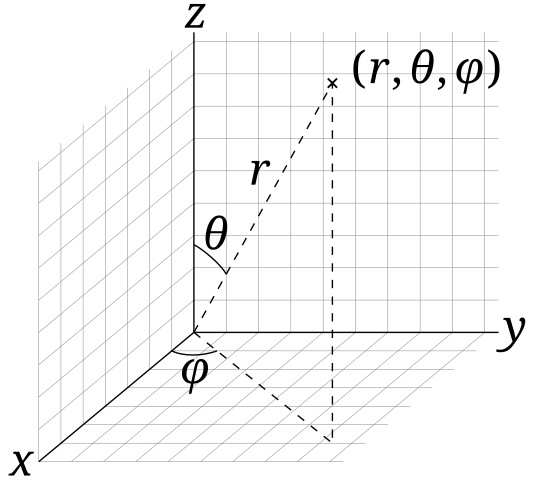
忽略掉 $r$，然后将 $\theta$ 和 $\varphi$ 放到 $[0,1]$ 中就能得到 $uv$ 坐标了：

但是当 $\varphi$ 为 $0$ 或 $2\pi$ 时，二者表示同一值，所以说会有不连续的空隙

球面坐标除了极点之外都是双射的

柱坐标

对于圆柱体，使用柱坐标即可

与球面坐标相似，转化为柱坐标并且去掉 $r$（这里 $z\in[-1,1]$）：

立方体贴图（Cubmaps）

球面坐标在两极附近有很严重的失真

常见的替代方法是：投射到一个立方体上，然后对立方体的六个面使用六个独立的正方形纹理。六个正方形纹理的集合称为立方体贴图（cubemap）

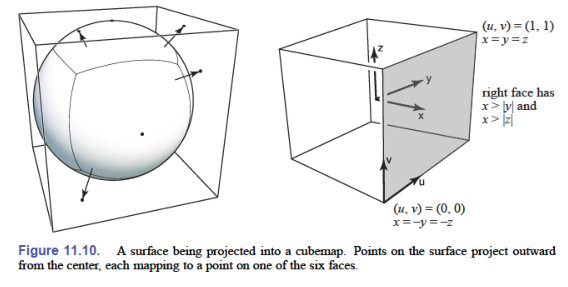
如何把球划分为六个面？眼睛在球心向外看，划分的线与立方体的棱重合

对于一个球心在原点的单位球：

这几个式子怎么得到的呢？我们看 $+x$ 的那个面

对于球面上一点 $(x,y,z)$，它对应的 $x=1$ 平面上的点坐标为（将 $x$ 坐标变成 $1$）：

我们再将转化为 $uv$ 坐标（从 $[-1,1]$ 到 $[0,1]$）：

上面的式子可能是为了统一，将 $u$ 和 $v$ 互换了一下？然后加上绝对值，正负号放到分母上，就是上面的几个式子

插值的纹理坐标

在三角形重心坐标系中，与其他属性一样可以进行插值

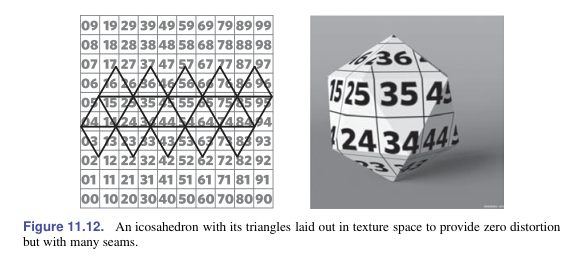
让纹理空间中的三角形面积与它们在 3D 中的面积成比例，可以使得形状的失真降低

平铺（Tiling）、环绕模式（Wrapping Modes）与纹理变换

允许纹理坐标超出边界通常很有用：

• 由于浮点数的精度问题，四舍五入可能越界
• 如果想要纹理只覆盖一部分表面，可以放大纹理坐标，例如 $[-4.5,4.5]^2$，此时纹理只覆盖 $[0,1]^2$ 这个区域

超出的部分可以设置背景色，或者进行 clamp

可以使用循环索引来实现重复的图案

通过选择环绕模式（wrapping mode，通常包括平铺、clamp、二者的组合）来指定纹理查找的方式，这样就能得到所有点的颜色

纹理坐标函数可以写成这样的形式：

连续性（Continuity）和接缝（Seams）

不连续性通常是不可避免的。对于任何闭合的 3D 曲面，没有连续的双射函数将整个曲面映射到纹理图像是拓扑学的常识。

插值时接缝需要特别考虑，不要让三角形横跨接缝，办法是加上 $2\pi$ 之类的（例如三个顶点是 $1.5\pi$、$1.9\pi$、$0.1\pi$，我们就可以把第三个顶点变成 $2.1\pi$）

渲染系统中的纹理坐标

一般来说纹理坐标存储在三角形顶点的属性中，其他图元（如球形）有预定义的纹理坐标，可以为其选择映射方案

• 光线追踪渲染器中，不仅要计算交点，还要计算交点的纹理坐标，存储在 Record 中，三角形图元插值，其他片元几何计算
• 光栅化渲染系统中，三角形通常是唯一支持的几何类型

抗锯齿纹理查找

不要在纹理的点上采样，要在纹理的一个区域内采样（面积均值）

在表面存在纹理的情况下有效地计算该面积均值是纹理抗锯齿的第一个关键主题

像素足迹（Footprint）

由于渲染的图像和纹理之间是个动态关系，所以很复杂

像素的纹理空间足迹（texture space footprint）

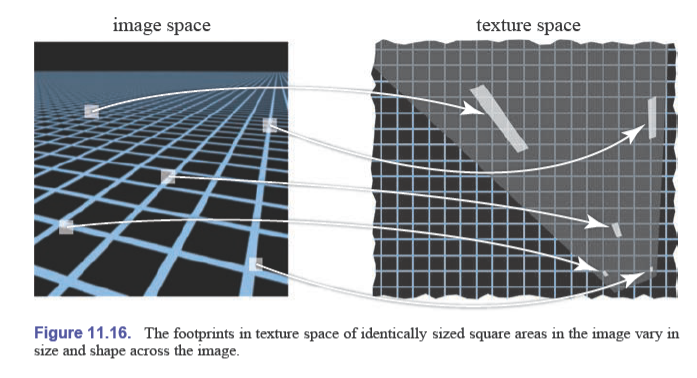
投影变换视为 $\pi$，那么从标准视空间变换回相机空间就是 $\pi^{-1}$，由于其他操作都是线性变换，我们先认为从 screen space 变回 object space 就是 $\pi^{-1}$

纹理坐标函数是 $\phi$，它是从 object space 映射到 texture space 的函数

那么从 screen space 到 texture space 的（大致的）变换就是 $\psi =\phi\circ \pi^{-1}$（函数复合）。由此，我们知道纹理空间足迹取决于视角情况和纹理坐标函数

我们也可以进一步大致上认为，image space 上的点（二维）也可以映射到 screen space（三维），所以我们将 image space 到 texture space 的函数也看成 $\psi$

这样太复杂，我们要找近似

当函数平滑时（$\psi$ 导数连续），使用线性近似：

其中 $\mathbf J$ 是：

这个式子表示了将一个曲面四边形区域近似为一个平行四边形，并且将均值近似为平行四边形中点的值

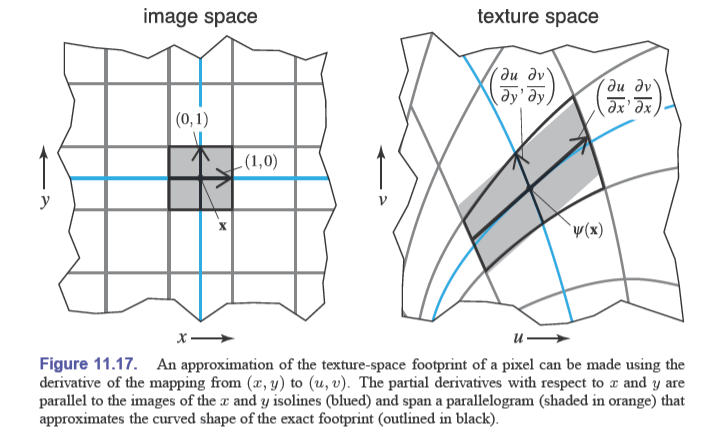
上面的就是一种过滤纹理采样（filtered texture sample）

纹理抗锯齿和纹理坐标查找的近似在速度和质量的权衡有所不同

重建

上采样：纹理足迹小于纹理元（texel）时，需要放大纹理，这是就是上采样。

纹理的上采样和图像的上采样一样要进行插值来进行平滑，这个平滑过程由重建滤波器定义（实际上纹理就是图像，对离散的图像进行重建），但与图像不同的是图像是规则的网格，纹理足迹是不规则的

上采样的情况下纹理网格（应该就是远处的那些点点）不明显

最高质量的是双线性插值（bilinear interpolation）

双线性插值的计算与图像中的相同，首先得到采样点在纹理空间的坐标，然后取四个相邻的纹理元进行线性平均

Color tex_sample_bilinear(Texture t, float u, float v) {
    u_p = u * t.width - 0.5
    v_p = v * t.height - 0.5
    iu0 = floor(u_p), iu1 = iu0 + 1
    iv0 = floor(v_p), iv1 = iv0 + 1
    a_u = (iu1 - u_p), b_u = 1 - a_u
    a_v = (iv1 - v_p), b_v = 1 - a_v
    return a_u * a_v * t[iu0][iv0] + a_u * b_v * t[iu0][iv1] +
           b_u * a_v * t[iu1][iv0] + b_u * b_v * t[iu1][iv1]
}

很多系统中，这是个性能瓶颈，主要是因为从纹理数据中获取四个纹理值所涉及的内存延迟。

高性能系统有专门用于纹理采样的硬件，用于处理插值和管理最近使用的纹理数据的缓存

线性插值可能不是一个足够平滑的重建，但是可以使用一些滤波器来采样到更高的分辨率

Mipmapping

在纹理足迹小于纹理元时，需要放大纹理

而在纹理足迹覆盖多个纹理元时，需要进行抗锯齿，前面说可以计算区域的面积，但是非常 expensive，更好的方法是预先计算和存储纹理在不同大小和位置的各个区域上的平均值。

一个常用的方法就是 mipmap，它是包含相同的图像，但分辨率越来越低的一系列纹理。

分辨率一般是一直除以 $2$，例如 level 0 是 $1024\times 1024$，level 1 是 $512\times 512$，以此类推

这种结构叫做图像金字塔（image pyramid）

使用 Mipmap 的基本纹理过滤（Texture Filtering）

对于面积为 $D$ 的纹理足迹，求出 $k=\log_2D$，然后有两种方式来近似计算面积均值：

• 只查找最接近 $k$ 的整数的值（效率高，但在 level 之间的突然转换时产生接缝）
• 查找最接近 $k$ 的两个整数的值，并对值进行线性插值（工作量增加一倍，但更平滑）

当纹理足迹非正方形时，需要确定哪一个当成 $D$，一个容易计算的是使用长边（$u$ 和 $v$ 的跨度取较大值）

书上伪代码，直接复制了：

Color mipmap_sample_trilinear(Texture mip[], float u, float v, matrix J) {
    D = max_column_norm(J)
    k = log2(D)
    k0 = floor(k), k1 = k0 + 1
    a = k1 - k, b = 1 - a
    c0 = tex_sample_bilinear(mip[k0], u, v)
    c1 = tex_sample_bilinear(mip[k1], u, v)
    return a * c0 + b * c1
}

基本的 mipmapping 在消除混叠方面做得很好，但它无法处理拉长或各向异性的像素足迹。

各向异性过滤（Anisotropic Filtering）

mipmap 可以与多个查找一起使用，以更好地近似延长的占用空间。

基于最小的轴来选择 mipmap 级别而非最长轴，然后将长轴上多个级别的采样求均值。

纹理映射的应用

用处仅仅受限于想象力

控制着色参数

漫反射颜色、镜面反射、镜面粗糙度等参数也可以用纹理表示

法线贴图（Normal Maps）与凹凸贴图（Bump Maps）

着色法线没有必要与表面的几何法线一致

将法线存储在纹理中，在每个纹理中存储三个数字表示法向量，而不是作为颜色 RGB

在对象空间中的法线映射是和表面几何关联的。要想正确显示法线映射的效果，法线的方向需要与表面的几何法线保持一致，如果表面发生变化或变形，法线映射的内容也应随之调整

解决方法是为表面上的每个点定义一个局部坐标系，这个局部坐标系会随着表面的变形而变化，常用的是切空间（tangent space）：

• 曲面上的某一点，选取一对切向量来定义一个标准正交基，切向量来源于纹理坐标（例如 $u$ 和 $v$ 坐标），它们分别对应于纹理在两个方向上的切线
• 通过正交化的方法将它们调整为正交基，从而构建一个局部的正交坐标系

在这种基（切线空间）下表示法线时，法线的变化会更加平滑稳定，变化会很小，靠近法线映射中的向量 $(0,0,1)^\mathrm T$。

使用凹凸贴图来间接指定法线

凹凸贴图是一个高度场：一个函数，它给出了光滑表面之上的细节表面的局部高度

从凹凸贴图中导出法线贴图很简单

置换贴图（Displacement Maps）

法线贴图实际上不会改变表面，只与着色有关

纹理不仅可以用于阴影，还可以用于改变几何形状，置换贴图是最简单的版本

使用单通道给出高于“平均地形”的高度，置换贴图实际上改变了表面，将每个点沿着光滑表面的法线移动到一个新的位置

实现置换贴图最常见的方法是：

• 首先将表面用许多小三角形细分（镶嵌，tessellation），这样可以生成一个更精细的网格，以便让更多的顶点可以移动
• 在顶点着色阶段，从置换贴图中获取置换值，直接修改顶点的位置

对地形来说特别方便

阴影贴图（Shadow Maps）

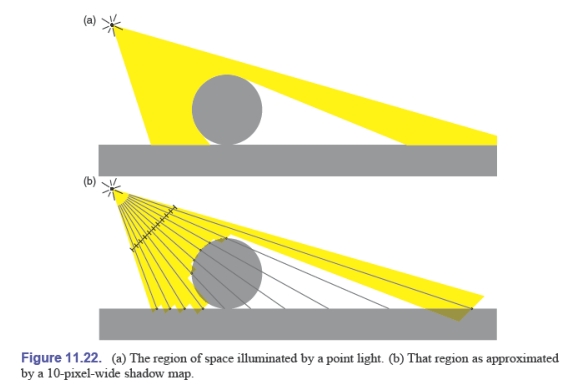
在光栅化渲染中获得阴影并不容易，阴影贴图是一种利用纹理贴图的机制从点光源中获得阴影的技术

阴影与物体对于相机的可见性这两个议题相似

在可见性情况下，使用 z-Buffer，而在阴影情况下使用阴影贴图

阴影贴图提前在单独的渲染通道中计算，里面存储了到整个场景中最近表面的距离

计算完阴影贴图后，执行普通的渲染过程，如果距离相同，则照亮片元，如果 $d > d_\text{map}$，这意味着有另一个表面更接近源，所以它是阴影

距离相同的判断需要一个误差 $\epsilon$，这个误差叫做阴影偏差（shadow bias），当 $d - d_\text{map}<\epsilon$ 是视为距离相同

在阴影贴图中查找时进行插值意义不大（可能会在平滑区域产生更准确的深度，但是在边界处会导致更大的问题），通常使用最近邻重建（nearest-neighbor reconstruction）来查找

但是为了避免走样，也可以使用百分比更接近过滤（percentage closer filtering）：小范围内多次采样，取平均，得到 $[0,1]$ 直接的值

环境贴图（Environment Maps）

环境贴图可以表示照明对于方向的依赖

将照明效果表示为单位球面上的函数，类似于使用纹理贴图表示球体表面的颜色变化

纹理坐标是通过观察方向的单位向量的坐标来计算，表示“从该方向观察时的光照效果”

环境图最常见的应用是在光线追踪中，为未击中任何物体的光线赋予颜色，充当背景。并且对于镜面物体来说，可以反射背景环境

类似的效果可以通过在光栅化中添加镜像反射来实现：

shade_fragment(view_dir, normal) {
    out_color = diffuse_shading(k_d, normal)
    out_color += specular_shading(k_s, view_dir, normal)
    u, v = spheremap_coords(reflect(view_dir, normal))
    out_color += k_m * texture_lookup(environment_map, u, v)
}

这种称为反射映射（Reflection Mapping），让光滑物体在光栅化环境中反射背景环境

环境贴图的一个更高级的用途是计算来自环境贴图的所有照明，而不仅仅是镜面反射。叫做环境光照（environment lighting）

可以在光线跟踪器中使用蒙特卡罗积分（Monte Carlo integration）或在光栅化渲染中使用光源的集合近似环境（一组分布在场景中的虚拟点光源）并计算许多阴影图。不懂

环境贴图可以放在球坐标或者 cubemap 中

程序化 3D 纹理（Procedural 3D Textures）

3D 纹理定义 3D 空间中每个点的 RGB 值，纹理映射比 2D 要简单

3D 纹理的缺点是将它们存储为 3D 栅格图像或体积会消耗大量内存，所以通常存储数学过程而不是栅格化后的纹理

2D 也可以使用程序化，但是通常还是存储栅格化纹理

3D 条纹纹理（3D Stripe Textures）

最简单的是两个颜色 $c_0$、$c_1$ 交替

RGB stripe(point p)
    if (sin(x_p) > 0) then
        return c0
    else
        return c1

如果想控制宽度：

RGB stripe(point p, real w)
    if (sin(pi * x_p / w) > 0) then
        return c0
    else
        return c1

如果想要线性渐变：

RGB stripe(point p, real w)
    t = (1 + sin(pi * x_p / w)) / 2
    return (1 - t) * c_0 + t * c_1

实噪音（Solid Noise）和湍流（Turbulence）

不看了，好像没什么用