图形学中许多应用需要对不寻常的空间进行“公平”采样
例如在像素中生成随机边，或者在像素中根据概率密度函数随机采样
本章提供了这一类概率运算的机制，这些机制对于蒙特卡罗积分也很有用
测度（Measures）与积分（Integration）
测度（measure）是一种将几何空间的度量（长度、面积、体积）和其他常见概念（如大小、质量和事件的概率）广义化后产生的概念
测度实际上是幂集（power set）到 $\mathbb R^+$ 的函数
例如二维平面的面积 $A$ 即平面点集的幂集到 $\mathbb R^+$ 的函数：
$$ A:\mathcal P(\mathbb R^2)\mapsto \mathbb R^+ $$其中，$\mathcal P$ 表示幂集，我们可以这样使用这个函数：
$$ A([a,a+1]\times[b,b+1])=1 $$这表示这块区域的面积为 $1$。
另外，$\emptyset$、单个点 $(x,y)$ 也是 $\mathbb R^2$ 的子集，但是它们的测度是 $0$，即：
$$ A(\{(x,y)\})=0\\ A(\emptyset)=0 $$还有一些集合的测度是 $0$，例如 $S=\{(x,y_0)\}$，其中 $x=1,2,\dots,N$，这些测度为 $0$ 的集合称为零测集（zero measure sets）
知道这个例子之后，我们来看测度这个概念，对于一个函数 $\mu$：
$$ \mu:\mathcal P(\mathbb S)\mapsto\mathbb R^+ $$如果 $\mu$ 是测度，那么它必须满足以下两个条件：
空集的测度是 $0$，即：
$$ \mu(\emptyset) =0 $$两个不同集合的度量之和等于它们各自的度量之和，即：
$$ \mu(A\cup B)=\mu(A)+\mu(B)-\mu(A\cap B) $$
当我们计算测度时，我们可以使用积分（integration），例如对于集合 $S$，有：
$$ A(S)=\int_{\vec x\in S}\mathrm dA(\vec x) $$这其实很好理解，是普通积分的一个推广
如果我们有一个在集合 $\mathbb S$ 上的测度，我们总可以乘上一个非负函数 $w$：
$$ w:\mathbb S\mapsto \mathbb R^+ $$的方式来创建一个新的测度，这可以用积分来表示。
例如我们有一个在 $\mathbb R^2$ 上的测度 $A$ 来表示面积，我们可以进行积分：
$$ A(S)=\int_{\vec x\in S}\mathrm dA(\vec x) $$如果我们乘上一个平方和函数，就可以变成另一个测度 $A'$：
$$ A'(S)=\int_{\vec x\in S}\Vert\vec x\Vert^2\mathrm dA(\vec x) $$测度和均值（Averages）
平均值是测度真正发挥作用的地方
当我们选择了一个“自然”的测度和定义域之后，我们使用下面的式子来计算函数 $f$ 在区域 $S$ 下对于测度 $\mu$ 的均值：
$$ \text{average}(f,S,\mu)\equiv\frac{\int_{\vec x\in S}f(\vec x)\mathrm d\mu(\vec x)}{\int_{\vec x\in S}\mathrm d\mu(\vec x)} $$这种机制有助于解决看似困难的问题（在这种问题中选择合适的测度很困难，但是我们可以直接使用一些公式？）。这类问题通常被叫做积分几何（integral geometry）
剩下两章看不懂
连续概率（Continuous Probability）
连续随机变量（continuous random variable）
概率密度函数（probability density function，PDF）
期望（expected value）、方差（variance）
$$ V(x)=E(x^2)-[E(x)]^2 $$大数定理（Law of Large Numbers）
蒙特卡洛积分（Monte Carlo Integration）
本节描述了定积分的基本蒙特卡洛求解方法
给定一个函数 $f:S\mapsto \mathbb R$ 和一个随机变量 $x\sim p$，我们可以计算 $f$ 在某个区域 $S$ 中的期望：
$$ E(f(x))=\int_{x\in S}f(x)p(x)\mathrm dx $$这意味着，我们如果知道了随机变量的分布，就能求出相关的期望
实际上，这个积分并不好算，我们可以通过随机取样进行近似：
$$ E(f(x))\approx \frac{1}{N}\sum_{i=1}^Nf(x_i) $$在此之上，我们希望近似单个函数的积分，而不是 $f$ 与 $p$ 的乘积，我们可以令 $g(x)=f(x)g(x)$，代入得：
$$ \int_{x\in S}g(x)\mathrm dx\approx \frac{1}{N}\sum_{i=1}^N\frac{g(x_i)}{p(x_i)} $$其中，当 $g(x_i)>0$ 时，$p(x_i)$ 不能为 $0$
为了更好地进行估计，我们想要尽可能多的样本，并且希望 $g/p$ 有较低的方差（$g$ 和 $p$ 应该具有相似的分布，如果这两个函数有相似的分布，可以帮助确保样本更加均匀地分布在整个区域内，从而减少计算中引入的波动）
“智能地”选择 $p$ 被称为重要性采样（importance sampling）
从上面的式子中，还体现了蒙特卡洛积分的收益递减（diminishing return）性质
估计的方差与 $1/N$ 成正比（？），标准差与 $1/\sqrt N$ 成正比。由于误差与标准差相似，所以需要 $4$ 倍的采样才能让误差下降一半
另外一种减少误差的方法是将积分域 $S$ 划分为几个更小的域 $S_i$，这被称为分层采样（stratified sampling）
通常，每个 $S_i$（密度为 $p_i$）只进行一次采样，在这种情况下，估计值的方差为：
$$ var\left(\frac{1}{N}\sum_{i=1}^N\frac{g(x_i)}{p_i(x_i)}\right)=\sum_{i=1}^Nvar\left(\frac{g(x_i)}{p_i(x_i)}\right) $$可以证明，如果所有层都有相等的测度，则分层抽样的方差永远不会高于非分层抽样（？）：
$$ \int_{x\in S_i}p(x)\mathrm d\mu=\frac{1}{N}\int_{x\in S}\mathrm d\mu $$书上的例子，关于分层采样与重要性采样的方差：
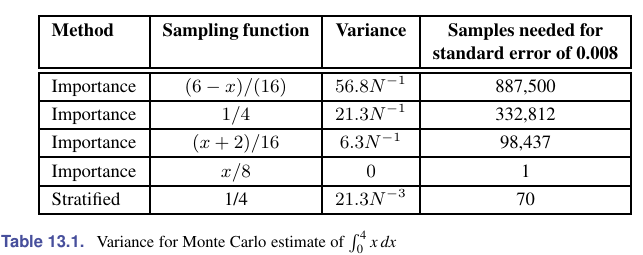
分层采样往往比重要性采样要好（在某些方面也有例外，如白噪声）
没有良好的结论说明分层采样与采样数的关系
伪蒙特卡洛积分（Quasi–Monte Carlo Integration）
一种流形的求积分的方法就是将蒙特卡洛积分中的随机点替换为伪随机点（quasi-random points），这些点是确定的，但在某种意义上是均匀的
例如，在一个单位面积区域 $S$ 中有 $N$ 个伪随机点，那么其中面积为 $A$ 的子区域中点的数量应该大概为 $AN$
伪随机点可以提高性能，但是要小心走样
求函数均值需要均匀采样，这时可以使用伪随机点
选择随机点
我们经常希望在单位正方形上生成一组随机或伪随机点，用于射线跟踪等应用。有几种方法可以做到这一点，例如抖动（jittering）
有时采样空间并不是正方形（例如圆形透镜），也可能不均匀（例如一个像素上的滤波函数？）
我们需要输入 $(u_i,v_i)$，通过一个函数，输出成目标空间中一组均匀的点
例如，如果我们定义一个函数，从 $(u_i,v_i)$ 到圆盘上的点 $(\phi_i,r_i)$：
$$ \phi_i=2\pi u_i\\ r_i=v_iR $$这有一个问题，就是这些点不均匀，我们需要某些方法来让它是均匀的，下面会介绍三种：函数反转（function inversion）、排斥 （rejection）和 Metropolis
函数反转（Function Inversion）
对于定义在区间 $x\in[x_\text{min},x_\text{max}]$ 上的一维密度函数 $f(x)$，我们可以从一组均匀的单位（uniform）随机数 $\xi_i$（$\xi_i\in[0,1]$）中生成随机数 $\alpha_i$
为了做到这样，我们需要累积分布函数 $P(x)$，有下面的等式：
$$ P(\alpha_i)=P_\xi(\xi_i) $$因为是均匀的单位随机数，所以：
$$ P(\alpha_i)=\xi_i $$所以：
$$ \alpha_i=P^{-1}(\xi_i) $$如果 $P(x)$ 不可逆（解析可逆），我们使用数值方法就足够了（不知道怎么求）
然后对于二维的来说，有所不同，我们先使用边缘分布函数 $F(x,y_\text{max})$，选择一个 $x_i$（应该是随便选一个就行），然后根据 $F(x_i,y)/F(x_i,x_\text{max})$ 选择 $y_i$
如果密度函数 $F(x,y)$ 可分离，即可以分成 $F(x,y)=F_x(x)F_y(y)$，那么我们可以在每一维上求逆得到相应的秩
例如，对于之前的圆盘，我们有：
$$ F(r,\phi)=\int_{0}^\phi\int_{0}^r\frac{r'}{\pi R^2}\mathrm dr\mathrm d\phi=\frac{\phi r^2}{2\pi R^2} $$这时：
$$ F(r,\phi)=\frac{r^2}{R^2}\times\frac{\phi}{2\pi} $$那么我们就能得到均匀的采样点：
$$ \phi=2\pi\xi_1\\ r=R\sqrt{\xi_2} $$另外一个例子，在渲染方程中，需要根据密度选择单位半球上的点：
$$ p(\theta,\phi)=\frac{n+1}{2\pi}\cos^n\theta $$其中 $n$ 是类似 Phong 的指数，$\theta$ 是表面法线的角度，$\theta \in[\theta, \pi/2]$（位于上半球），$\phi$ 是方位角 ($\phi \in [0, 2\pi]$)
累积分布函数为：
$$ P(\theta,\phi)=\int_0^{\phi}\int_0^{\theta}p(\theta',\phi')\sin\theta'\mathrm d\theta'\mathrm d\phi' $$其中 $p$ 可分离，所以 $P$ 可分离，所以可以使用前面的方法，得到：
$$ \theta = \mathrm{arccos}\left[(1 − \xi_1)^{\frac{1}{n+1}}\right]\\ \phi = 2\pi\xi_2 $$单位正方形上的一组抖动点（jittered points，这个之前提过好几次，我怎么不记得第四章说过）可以很容易地转换为具有所需分布的半球上的一组抖动点
通常，我们必须将球面上的点映射到 $uvw$ 基上的合适方向，为此我们经常将角度转化为单位向量 $\vec a$：
$$ \vec a=(\cos\phi\sin\theta,\sin\phi\sin\theta,\cos\theta) $$为了提高效率，我们可以不使用反三角，例如当 $n=1$ 时向量 $\vec a$ 可以被简化为：
$$ \vec a=\left(\cos(2\pi\xi_1)\sqrt{\xi_2},\sin(2\pi\xi_1)\sqrt{\xi_2},\sqrt{1-\xi_2}\right) $$这里应该说的是不使用 $\phi$、$r$ 而使用三维笛卡尔坐标系
排斥（Rejection）
拒绝方法根据一些简单分布选择点，并拒绝一些分布更复杂的点，有几种使用拒绝的场景
假设我们希望单位圆内的均匀随机点。我们可以选择均匀随机点 $(x, y) \in [−1, 1]^2$ 并拒绝圆外的点
尽管拒绝方法通常对代码简单，但它与分层不兼容，它收敛得更慢，因此应该主要用于调试或特别困难的情况
Metropolis
https://www.bilibili.com/video/BV1iG4y1w7sP
Metropolis 方法使用随机突变（random mutations）来生成一系列具有所需密度的采样点
马尔可夫链（Markov Chain）
如果对于随机变量 $\{x^{(t)}\}_{t=0,1,2,\dots}$，满足：
$$ P\{x^{(t)}|x^{(1)},x^{(2)},\dots,x^{(t-1)}\}=P\{x^{(t)}|x^{(t-1)}\} $$也就是具有 one-step dependence，就称其为马尔可夫链
其中，这个性质叫做马尔科夫性（Markov property），$P\{x^{(t)}|x^{(t-1)}\}$ 被称作转移概率（transition probability）
为了方便，我们记：
$$ p_{ij}^{(t)}=P\{x^{(t+1)}=j|x^{(t)}=i\} $$表示在 $t$ 时刻，从状态 $i$ 转移到状态 $j$ 的概率
如果其与时间 $t$ 无关，那么称其为时齐（time-homogeneous）马尔可夫链，上面的那个 $p$ 记为 $p_{ij}$
马尔可夫链的平稳分布（Stationary Distribution）
从极限的角度理解，表示为：
$$ \lim_{n\to \infty}P\{x^{(t+n)}=j|x^{(t)}=i\}=\pi_j $$表示当转移次数足够多时，无论从什么状态转移，转移到状态 $j$ 的概率均为 $\pi_j$，叫做状态 $j$ 的平稳概率
平稳概率与初始状态无关
如果直接从定义的角度出发，其实就是 OI 中的概率 DP 那个部分，写成一个方程组：
$$ \sum_{i=1}^{|S|}p_{ij}\pi_i=\pi_j $$满足这些等式的状态叫做平稳状态（stationary state）
如果对于任意 $i$ 和 $j$，满足：
$$ \pi_ip_{ij}=\pi_jp_{ji} $$也就是说，$i$ 转移到 $j$ 的概率和 $j$ 转移到 $i$ 的概率相同
那么称满足可逆性（reversible property）