- 光子(Photons)
- 光滑金属(Smooth Metals)
- 光滑电介质(Smooth Dielectrics)
- 拥有次表面反射(Subsurface Scattering)的电介质
- 暴力求解的光子追踪器(Photon Tracer)
- 辐射度量学(Radiometry)
- 辐射能量(Radiant Energy)
- 辐射通量(Radiant Flux)或功率(Power)
- 其他感兴趣的度量概念
- 立体角(Solid Angle)
- 微分(Differential)立体角
- 辐射强度(Radiant Intensity)
- 辐照度(Irradiance)
- 辐射(Radiance)或亮度(luminance)
- 辐照度与辐射之间的联系
- 散射的辐射度量
- 实际中的材质
- 蒙特卡洛光线追踪
虽然所有的渲染都是“基于物理的”,但是这里的“基于物理”意味着严格地遵循物理模型,而不是基于经验的
光子(Photons)
本章使用大量光子的集合来描述辐射度量,图形学中的光子与物理学不太一样,在这里,光子通常只是一个携带能量的包裹,它的行为方式服从几何光学,不具有波动性
更准确地说,对我们而言,光子是一束光,它有位置、传播方向、波长 $\lambda$ 和速度 $c$。
光的速度 $c$ 只取决于介质的折射率 $n$
$f=c/\lambda$,在不同的介质中,$f$ 不变,$\lambda$ 和 $c$ 改变
光子携带的能量 $q$ 在不同的介质中也不变,$q=hf=\frac{hc}{\lambda}$,其中 $h=6.63\times 10^{-34}J\cdot s$ 是普朗克常数(Plank’s Constant)
光滑金属(Smooth Metals)
对于光滑金属来说,光要么被镜面反射(reflect specularly)要么被折射到表面(refract into the surface),然后被迅速吸收(薄涂层金属就像玻璃一样,有时并不是完全不透明的)
反射光的量由菲涅尔方程(Fresnel equations)来决定。它的值随着光的偏振(polarization)而变化,随着入射角增加,反射率增加。在接近入射余角(grazing angle)时达到 100%
对于金属来说,我们一般指定正入射(沿着法线方向)时的反射率为 $R_0(\lambda)$,一个很好的近似(Schlick)是:
$$ R(\theta,\lambda)=R_0(\lambda)+(1-R_0(\lambda))(1-\cos\theta)^5 $$其中,$\theta$ 是入射光与法线的夹角
光滑电介质(Smooth Dielectrics)
电介质是一种能折射光线的材料
有一种很好的启发式的记忆方法——如果材料不是金属,那它就是电介质。 因此,皮肤、牛奶、头发、布料和几乎所有日常材料都是电介质
由于它们是不同折射率和吸光杂质的混合物,这些材料往往是不透明的。但是,光滑均匀的电介质(匀质)是透明的,例如玻璃、水和眼睛里的晶状体。
对于光滑的电介质,只有三个重要的属性:
- 在不同的入射角和波长下,多少光被反射
- 当光以给定的距离和波长穿过材料时,有多少被吸收(衰减)
- 反射光和折射光的方向是什么
电介质的反射率(Reflectivity)
光的几何弯曲以及反射/折射的比例取决于材料的折射率 $n(\lambda)$
对于电介质,反射率也可以像光滑金属一样使用菲涅尔方程(Schlick)来计算
当两侧介质中有一个是空气,另一个是折射率为 $n(\lambda)$ 的电介质时,用下面的式子表示 $R_0(\lambda)$:
$$ R_0(\lambda)=\left(\frac{n(\lambda)-1}{n(\lambda)+1}\right)^2 $$当两侧折射率都不是 $1.0$ 的情况下,这样计算:
$$ R_0(\lambda)=\left(\frac{n_t(\lambda)-n_i(\lambda)}{n_t(\lambda)+n_i(\lambda)}\right)^2 $$其中,$n_t$ 是折射光(transmit)所在介质的折射率,$n_i$ 是入射光(incident)所在介质的折射率
通常来说,折射率并不随波长变化
常用的折射率:水($n=1.33$)、玻璃($n=1.4$ 到 $1.7$)、钻石($n=2.4$)
透射的部分直接用能量守恒就能算出来
折射(Refraction)与 Beer 法则
电介质也会过滤和折射光。
折射定律(Snell’s law):
$$ n\sin\theta=n_t\sin\phi $$可以推导出余弦的式子:
$$ \cos^2\phi=1-\frac{n^2(1-\cos^2\theta)}{n_t^ 2} $$我们使用三维向量来表示,首先选择曲面法线与入射光所在平面,在上面建立二维正交基:
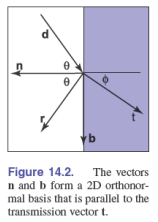
在这里,$\vec n$ 和 $\vec b$ 组成了一组二维正交基,用它俩表示入射光 $\vec d$ 和折射光 $\vec t$:
$$ \begin{aligned} \vec d&=\vec b\sin\theta-\vec n\cos\theta\\ \vec t&=\vec b\sin\phi-\vec n\cos\phi \end{aligned} $$加上折射定律:
$$ n\sin\theta=n_t\sin\phi $$现在我们需要用 $\vec d$ 和 $\vec n$ 来表示 $\vec t$:
$$ \begin{aligned} \vec t&=\vec b\sin\phi-\vec n\cos\phi\\ &=\left(\frac{\vec d+\vec n\cos\theta}{\sin\theta}\right)\sin\phi-\vec n\cos\phi\\ &=\left(\vec d+\vec n\cos\theta\right)\frac{n}{n_t}-\vec n\cos\phi\\ &=\frac{n(\vec d-\vec n(\vec d\cdot\vec n))}{n_t}-\vec n\sqrt{1-\frac{n^2(1-(\vec d\cdot n)^2)}{n_t^2}} \end{aligned} $$不管 $n$ 和 $n_t$ 哪个更大,这个方程都成立
当根号下数字为负时,称为全内反射(total internal reflection),所有的能量都被反射了
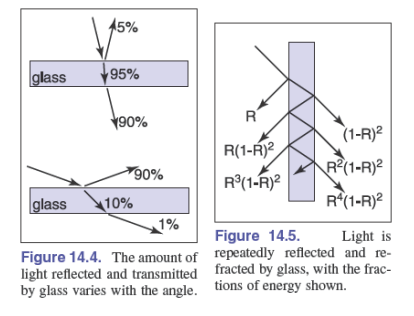
对于均匀的介质,例如有色玻璃,根据 Beer 定律,透射光线的强度将随着距离增大而衰减(attenuated),满足:
$$ \mathrm dI=-CI\mathrm dx $$其中 $x$ 表示距离。我们可以把它变成:
$$ \frac{\mathrm dI}{\mathrm dx}=-CI $$解这个微分方程可以得到:
$$ I=ke^{-Cx} $$通常,衰减程度由衰减常数 $a$ 表示,它是经过单位距离后的衰减量:
$$ \begin{aligned} I(s)&=I(0)a^s\\ a&=e^{-C} \end{aligned} $$下面是由于 Beer 定律的影响,而呈现绿色的玻璃:

这种效应也适用于透射光,光被反复折射和反射,通常只有一两个反射式是容易看到的
拥有次表面反射(Subsurface Scattering)的电介质
只需使用光滑的电介质,我们就可以渲染一系列令人惊讶的材料。许多看起来无光泽和不透明的表面可以模拟为多个电介质。考虑一个完美的冰块,它看起来像一块玻璃,只是其折射时扭曲光线的程度较小(冰的折射率比玻璃低)。现在在冰块内部放置许多小球形气穴,随着添加更多气泡,冰块将变得越来越不透明。
散射也许是我们所观察到的不透明现象的重要原因。使冰块看起来不透明的另一种方法是使表面变得粗糙。这可以在模型上通过细分表面然后对每个三角形顶点的位置进行小的扰动来完成。它的效果很像磨砂玻璃(本质上是那种粗糙的表面),扰动越粗糙,就会出现不透明度。
通过插入具有颜色的粒子可以实现进一步的复杂性,从而激活比尔定律。这是一个相当简单的模拟涂料的极其精确的方法。
我们能找到一大批材料,这些材料的复杂度可以通过显式建模它的微观结构来模拟。例如,人类皮肤可以建模为粗糙的表面和折射率略有不同的颜料颗粒层和血液(都遵守比尔定律)
暴力求解的光子追踪器(Photon Tracer)
暴力模拟光子、从传感器反向发送伴随(后向)光子
传感器(Sensor)
一个简单的传感器阵列,每个传感器都充当光子计数器(某些波长比其他波长引起更多的响应),当光子轰击时,根据光子的量产生一个灰度值
为了生成彩色图像,可以在传感器前以某种方式放置红绿蓝滤光片,最简单的滤波器是带通滤波器(bandpass filter):
- 蓝色:仅在 $\lambda\in[400,500\ \mathrm{nm}]$ 时有全响应(full response),其他均无响应
- 绿色:$\lambda\in[500,600\ \mathrm{nm}]$
- 红色:$\lambda\in[600,700\ \mathrm{nm}]$
如果将所有的传感器初始化为零,那么全响应意味着当光子击中传感器时增加传感器中值的大小
光子追踪器
为了追踪光子,在光源上随机选择一个点,随机选择一个方向和 400 到 700 nm 之间的随机波长。
当它碰到一个表面时,计算反射率 $R$,取一个均匀随机数 $\xi\in[0,1)$,执行:
if (ksi < R)
产生一个反射光子并且跟踪它
else
产生一个折射光子并且跟踪它
如果表面是金属的,那么光子在折射的情况下被吸收,然后我们在光源处生成一个新的光子
如果光子进入电介质,而比尔定律系数不是 1,那么光子可能会被吸收,所以执行:
if (ksi < 被吸收的概率)
吸收光子然后在光源处生成一个新的光子
else
允许光子在下一次击中时射出介质
运动(Motion)和散焦模糊(Defocus Blur)
上面的模拟将产生清晰的图像,但是需要长时间的曝光,因为很少有光子能够幸运地在被吸收之前打到传感器上
我们可以放弃前面的“针孔相机”,使用真正的摄像机,把针孔换成复合玻璃透镜或者一个理想的薄透镜:
最简单的玻璃透镜可以是两个球体的重叠部分(双凸球面透镜)。这有不错的成像特性(虽然不如大多数真实相机中的复合镜头好),并且很容易写出光线求交的代码
薄透镜是一种理想的透镜,它是无限薄的,只指定半径和焦距 $f$,所有射入的光线不弯曲地汇聚于焦点处,并且满足薄透镜的成像公式($1/a+1/b=1/f$)
使用真实或理想的镜头会自动产生真实照片中出现的那种模糊,通常称为散焦模糊(失焦)或景深(depth of field)。
反转时间
上面的光子追踪器可以工作并且工作得很好,只是会很慢,因为即使在你插入一个镜头之后,大多数光子也不会击中镜头
通常在图形程序中做的事情是反转时间,从相机发出射线,并在射线击中光源时记录下来
我们从每个像素发出光子(伴随光子,adjoint photons),看看它们在哪里碰到光源
辐射度量学(Radiometry)
上一节的暴力求解渲染器对于应用程序是不可行的,我们不要模拟微观几何,要模拟整体行为
辐射度量学中最重要的物理量是辐射率 Radiance
这里直接按照闫老师的 GAMES 101 来了,这本书上的概念(比如光谱能量)比较奇怪
辐射能量(Radiant Energy)
辐射能量是电磁辐射(electromagnetic radiation)的能量,单位是焦耳 $\mathrm J$,用 $Q$ 来表示
辐射通量(Radiant Flux)或功率(Power)
辐射通量(或功率):单位时间发射(emitted)、反射(reflected)或接受(received)的能量,单位是瓦特 $\mathrm W$ 或者流明(lumen)$\mathrm {lm}$,通常表示如下:
$$ \Phi\equiv\frac{\mathrm dQ}{\mathrm dt} $$也可以理解为:给一个平面,单位时间内通过该平面的光子的数量
其他感兴趣的度量概念
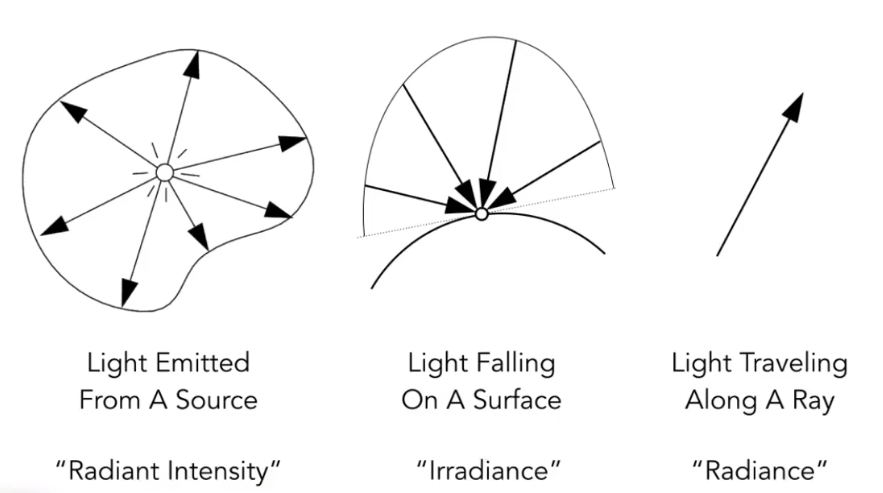
由于光会向四面八方辐射能量,所以会定义一个与方向有关的概念,即辐射强度(Radiant Intensity)
反过来,我们可能想要知道接受的能量与方向的关系,这个概念是辐照度(Irradiance)
光沿着直线传播,度量光传播过程中的能量我们用概念辐射(Radiance)
立体角(Solid Angle)
在二维中,角度(Angle)为圆上的弧长与半径的比值,即:
$$ \theta=\frac{l}{r} $$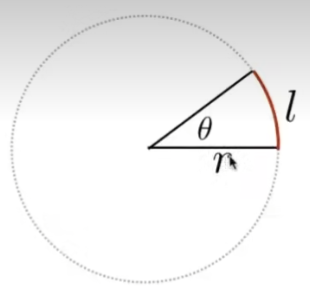
我们知道,一个圆的周长是 $2\pi r$,所以整个圆有 $2\pi$ 弧度(radians),弧度是角度的单位
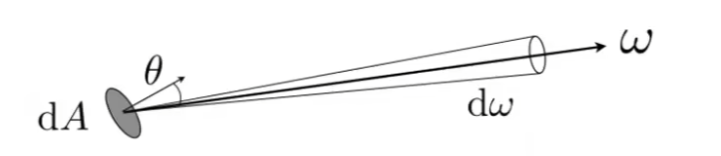
立体角是角度在三维空间中的延伸,它表示为球面上的面积与半径的平方($r^2$)的比值,即:
$$ \Omega=\frac{A}{r^2} $$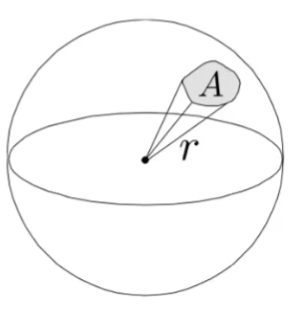
一个球的表面积为 $4\pi r^2$,所以一个球共有 $4\pi$ 球面度(steradian),球面度是立体角的单位,记作 $\mathrm {sr}$
微分(Differential)立体角
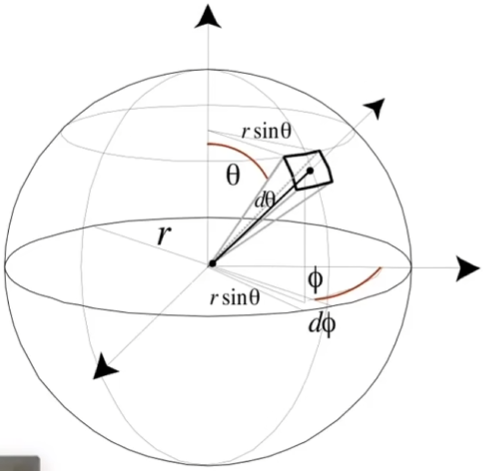
在高数中,我们知道球面上的单位面积可以表示为:
$$ \mathrm dA=r^2\sin\theta\mathrm d\theta\mathrm d\phi $$其中,$\theta$($\theta\in[0,\pi)$)是与 $y$ 轴的夹角,$\phi$($\phi\in[0,2\pi)$)是与 $x$ 轴的夹角
根据立体角的定义,我们也可以求出立体角的微分:
$$ \mathrm d\omega=\frac{\mathrm dA}{r^2}=\sin\theta\mathrm d\theta\mathrm d\phi $$我们验证一下,把整个球面的立体角的微分积起来,可以得到:
$$ \Omega=\int_{S^2}\mathrm d\omega=\int_{0}^{2\pi}\int_{0}^{\pi}\sin\theta\mathrm d\theta\mathrm d\phi=4\pi $$其中,$S^2$ 表示单位球
这里的 $\omega$ 表示立体角,如果是向量形式的 $\vec{\omega}$,那么就表示立体角的方向(单位向量)
辐射强度(Radiant Intensity)
辐射强度:单位立体角(solid angle)由点光源发出的功率(power),即:
$$ I(\vec \omega)\equiv\frac{\mathrm d\Phi}{\mathrm d\omega} $$它的单位是:$\mathrm W/\mathrm {sr}$ 或者坎德拉(candela,$\mathrm {lm}/\mathrm {sr}$)
这里 $I$ 后面的 $\vec\omega$ 就表示立体角的方向
举一个例子,对于一个点光源来说,如果它发射的能量是均匀的(各向同性点光源,Isotropic Point Source),如果我们把辐射强度记为 $I$,那么:
$$ \Phi=\int_{S^2}I\mathrm d\omega=4\pi I $$也就是说:
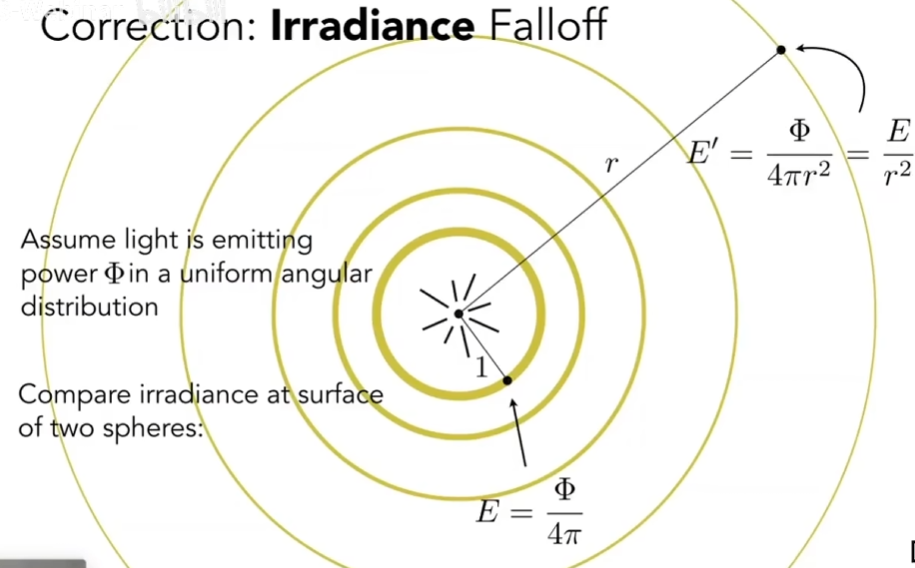
$$ I=\frac{\Phi}{4\pi} $$辐照度(Irradiance)
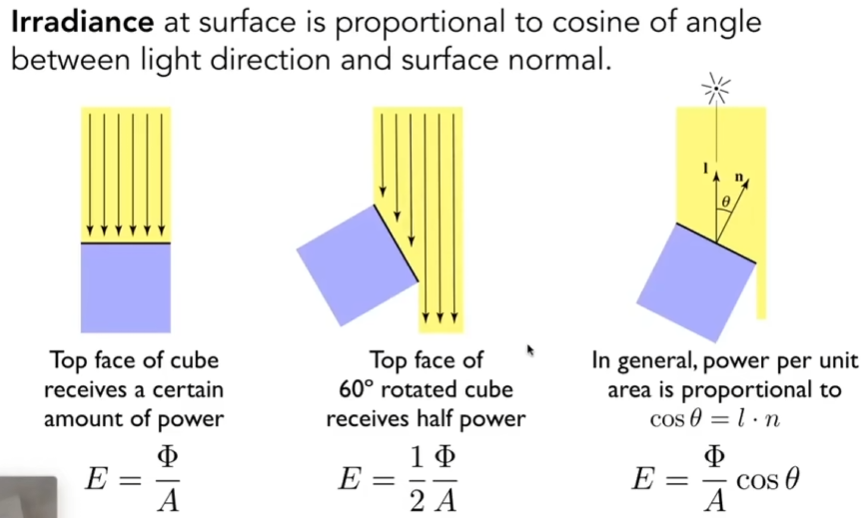
辐照度指的是每(需要垂直方向,如果不垂直需要进行投影)单位区域入射到一个表面上一点的辐射通量(功率),即:
$$ E(\vec x)\equiv\frac{\mathrm d\Phi(\vec x)}{\mathrm dA} $$理解:某处($\vec x$)有一个微小的面积,面积中的微小能量(功率)除以这个微小面积就是辐照度
它的单位是 $\mathrm {W}/\mathrm {m^{2}}$ 或者勒克斯 $\mathrm {lux}$($\mathrm {lm}/\mathrm {m^{2}}$)
这可以解释:朗伯余弦定律(Lambert’s Cosine Law,需要投影)、点光源的辐照度衰减(根据定义,除以球的面积,辐射强度没变)
辐射(Radiance)或亮度(luminance)
辐射是在单位立体角、单位面积上一个表面发射、反射或者传递的能量,表达式是:
$$ L(\vec p,\vec \omega)\equiv\frac{\mathrm d^2\Phi(\vec p,\vec \omega)}{\mathrm d\omega\ \mathrm dA\cos\theta} $$其中,$\cos\theta$ 表示的是面积的投影
它的单位是 $\mathrm W/\mathrm {sr}\ \mathrm {m^2}$ 或者尼特($\mathrm {nit}$,$\mathrm {cd}/\mathrm {m^2}$ 或 $\mathrm {lm}/\mathrm {sr}\ \mathrm {m^2}$)
理解:限定一个方向、限定一个微小面积
辐射可以将辐照度和辐射强度联系起来:
- 辐射是单位立体角上的辐照度
- 辐射是单位投影面积上的辐射强度
由此我们可以定义其他的概念
比如入射辐射(incident radiance),表示单位立体角、单位面积上到达表面的辐射,表达式是:
$$ L_i(\vec p,\vec \omega)=\frac{\mathrm dE(\vec p)}{\mathrm d\omega\cos\theta} $$这里的 $\cos\theta$ 表示的是立体角 $\vec\omega$ 与面积 $\mathrm dA$ 法线之间的夹角。和辐照度中的“垂直或投影”不是一个东西
出射辐射(exiting radiance),表示单位立体角、单位面积上到达发射的辐射,表达式是:
$$ L_e(\vec p,\vec \omega)=\frac{\mathrm dI(\vec p,\vec\omega)}{\mathrm dA\cos\theta} $$辐照度与辐射之间的联系
辐照度表示 $\mathrm dA$ 接收到的能量
辐射表示 $\mathrm dA$ 从 $\mathrm d\omega$ 方向接收到的能量
它们之间有一个联系,即之前的定义:
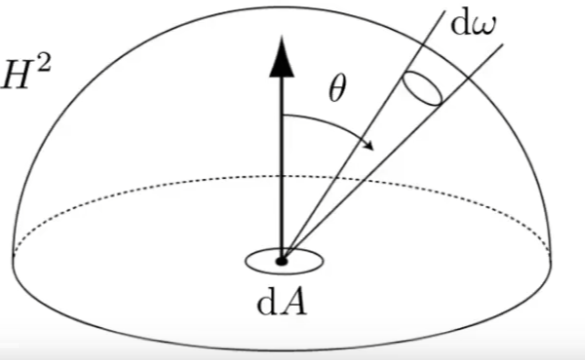
$$ \mathrm dE(\vec p,\vec\omega)=L_i(\vec p,\vec\omega)\cos\theta\mathrm d\omega $$我们可以两边积分:
$$ E(\vec p)=\int_{H^2}L_i(\vec p,\vec\omega)\cos\theta\mathrm d\omega $$其中,$H^2$ 表示单位半球
散射的辐射度量
对于粗糙的表面,我们不用实际性的几何形状来表示表面上微小的沟,而是统计性地表征它们
光滑的表面在多个方向上随机反射光线,就好像表面上有看不见的小细节一样。这个函数被称为双向反射分布函数(bidirectional reflectance distribution function,BRDF)
第二个概念是相位函数:说明光在任何给定的 3D 位置中散射的可能性有多大,被吸收的可能性有多大。以及散射光的方向分布是什么。该方向分布只是一个概率密度函数,称为体积的相位函数
BRDF
这里还是 GAMES 101
BRDF 表示了光从每个入射角度如何被反射到每个出射角度,表达式为:
$$ f_r(\vec{\omega_i}\rightarrow\vec{\omega_r})=\frac{\mathrm dL_r(\vec{\omega_r})}{\mathrm dE_i(\vec{\omega_i})}=\frac{\mathrm dL_r(\vec{\omega_r})}{\mathrm dL_i(\vec{\omega_i})\cos\theta_i\mathrm d\omega_i} $$单位是 $\mathrm{sr}^{-1}$
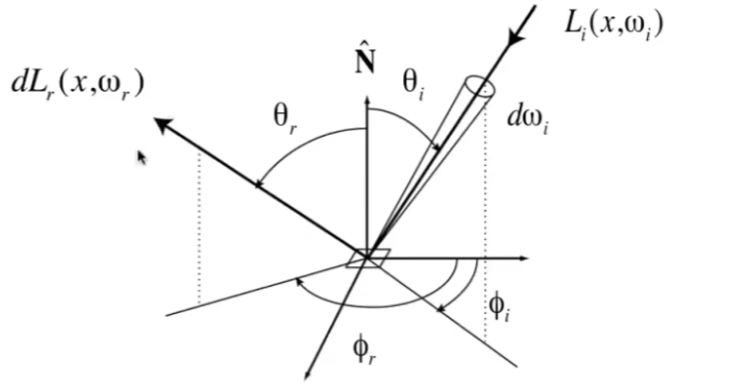
注意,它是一个辐射除以辐照度
反射方程(Reflection Equation)
一个对于所有入射方向的积分,得到某个反射方向的 radiance,这就是反射方程:
$$ L_r(\vec p,\vec{\omega_r})=\int_{H^2}f_r(\vec p,\vec{\omega_i}\rightarrow\vec{\omega_r})L_i(\vec p,\vec{\omega_i})\cos\theta_i\mathrm d\omega_i $$渲染方程(Rendering Equation)
光线可能弹射多次,一个物体的反射光线有可能称为另一个物体的入射光线,出现递归
渲染方程是:
$$ L_r(\vec p,\vec{\omega_r})=L_e(\vec p,\vec{\omega_r})+\int_{H^2}f_r(\vec p,\vec{\omega_i}\rightarrow\vec{\omega_r})L_i(\vec p,\vec{\omega_i})(\vec n\cdot\vec{\omega_i})\mathrm d\omega_i $$其中,$L_e(\vec p,\vec{\omega_r})$ 表示自发光项,$(\vec n\cdot\vec{\omega_i})$ 其实就是 $\cos\theta_i$
剩下的就不深入讨论了
关于传递方程(transport equation),这里也不看了
实际中的材质
在文献中有许多 BRDF 模型,并在行业中使用。有许多领域使用 BRDF 模型,包括遥感、传热、材料科学,当然还有计算机图形学。不幸的是,在这些领域没有一个标准的分类集,甚至在图形领域也没有。然而,这些是大多数人同意的一些分类标准,如下图:
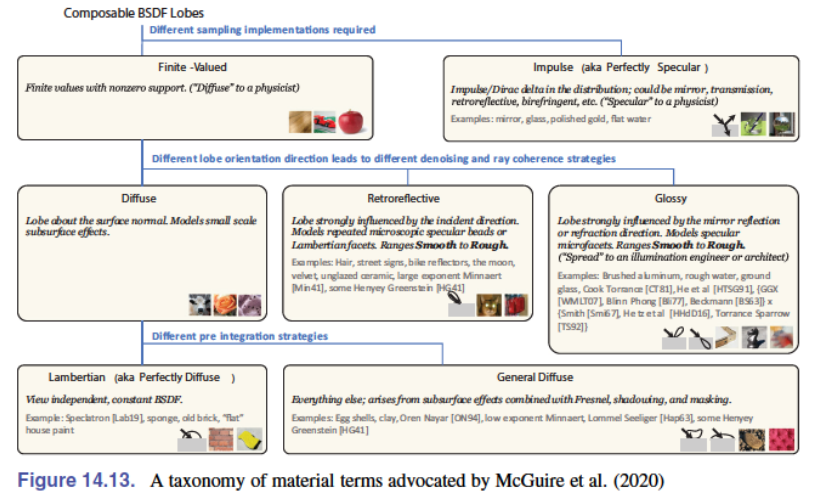
在行业中将材质分为这些类别,并为每个材质类型使用不同的 BRDF 模型。然后将这些材质类型与常数或由菲涅耳系数确定的简单权重结合起来
Burley/Disney 模型的变体
目前最主要的光泽 gloosy 形式是 GGX 微表面模型
蒙特卡洛光线追踪
根据前面的反射方程,我们可以使用蒙特卡洛积分来进行数值求解:
$$ \begin{aligned} L_r(\vec p,\vec{\omega_r})&=\int_{H^2}f_r(\vec p,\vec{\omega_i}\rightarrow\vec{\omega_r})L_i(\vec p,\vec{\omega_i})\cos\theta_i\mathrm d\omega_i\\ &\approx\frac{1}{N}\sum_{i=1}^{N}\frac{f_r(\vec p,\vec{\omega_i}\rightarrow\vec{\omega_r})L_i(\vec p,\vec{\omega_i})\cos\theta_i}{p(\vec{\omega_i})} \end{aligned} $$然后我们只需要找一个概率密度函数即可,可以使用半球面上的均匀分布
这里的光线追踪与本章前面开发的伴随光子追踪器非常相似。但推导方法不同,采用显式辐射积分法,可以得出相似的结论。