集合与映射
映射与函数（Function）是一回事
- $\mathbb R$：实数集
- $\mathbb R^+$：非负实数集（包括 $0$）
- $\mathbb R^2$：实二维平面的有序对集合
- $\mathbb R^n$：笛卡尔空间（二维直角坐标系构成的空间）中的 n 维点集
- $\mathbb Z$：整数
- $S^2$：单位球面的三维点集（是 $\mathbb R^3$ 的子集）
$S^2$ 可以映射到二维表面上，所以它可以由二维表示（向量组的秩是 2）
$f: \mathbb R\mapsto\mathbb{Z}$ 是一个映射，左边称为定义域（domain），右边称值域（target），$f(a)$ 称为 $a$ 的像（image）
反函数、双射（正反映射均唯一）
三角函数
三角函数、弧度、角度、反三角（尤其是 atan2: $\mathbb R^2\mapsto[-\pi, \pi]$）、三角公式
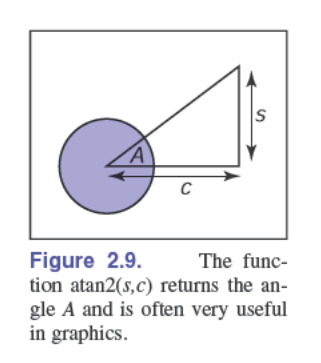
面积公式：
$$ S=\frac{1}{4}\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)} $$大圆（单位球上的中心点在原点的圆弧）、球面三角函数（边都在大圆上的三角形）
立体角：平面角的定义是二维线条投影到单位圆上（线条上的点与圆心的连线与单位圆的交点集合）的长度大小，度量是 $2\pi$；立体角则是提升到了三维，是三维物体投影到单位球上的面积大小，度量是 $4\pi$
向量
向量、向量计算、点积、映射（用 $\vec{a}\rightarrow \vec{b}=\Vert \vec{a}\Vert \cos \phi=\frac{\vec{a}·\vec{b}}{\Vert \vec{b}\Vert }$ 表示）、叉乘（仅三维）、正交基、坐标系
从单个向量创建坐标系
从单个向量 $\vec{a}$ 创建局部坐标系：
$$ \vec{w}=\frac{\vec{a}}{\Vert \vec{a}\Vert }\\ \vec{u}=\frac{\vec{t}\times\vec{w}}{\Vert \vec{t}\times\vec{w}\Vert }\\ \vec{v}=\vec{w}\times\vec{u} $$从两个向量创建坐标系
从两个向量 $\vec{a}$（表示 $\vec{w}$，相机朝向）和 $\vec{b}$（表示 $\vec{v}$，指定相机的旋转）创建局部坐标系，通常只需要叉乘即可，但为了确保正交，鼓励再执行一遍从单个向量创建坐标系的流程，即：
$$ \vec{w}=\frac{\vec{a}}{\Vert \vec{a}\Vert }\\ \vec{u}=\frac{\vec{b}\times\vec{w}}{\Vert \vec{b}\times\vec{w}\Vert }\\ \vec{v}=\vec{w}\times\vec{u} $$这个方法非常有效，即使 $\vec{b}$ 与 $\vec{a}$ 不垂直，得到的 $\vec{v}$ 也是与 $\vec{b}$ 最接近的垂直于 $\vec{w}$ 的向量。
如果 $\vec{a}$ 与 $\vec{b}$ 共线，那么这个方法不能工作，叉乘是 $\vec{0}$
整理正交基
如果从精度较低的文件中读取正交基，可能会出现些微的误差，这时需要重新整理正交基。可以使用上面的方法，但上面的方法“偏爱” $\vec{w}$，因为 $\vec{w}$ 的方向始终准确，这就不太好。之后有一个叫 SVD 的方法来解决这个问题
积分
图形学中大多积分不需要解析解，且有明确的含义
平均和加权平均
关于立体角的积分（这个这边写的太晦涩了，看不懂积分式子，后面章节还会看到它）
（概率）密度函数
曲线和曲面
tips：尽量使用向量形式，包括代码上（例如圆的表示，不要用 $x$、$y$、$z$，而直接用向量）
隐式 2D 曲线：$f(x, y)=0$。梯度与法线向量（具体在《方向导数、梯度和法线向量》这一个笔记中）：$\nabla f(x,y)=\left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right)$
隐式 2D 直线：$Ax+By+C=0$。距离：$\text{distance}=\frac{f(a,b)}{\sqrt{A^2+B^2}}$，一般会将 $A$ 和 $B$ 归一化
隐式二次曲线：$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$，圆和椭圆
3D 隐式曲面：$f(x,y,z)=0$，向量形式 $f(\vec p)=0$。法线为 $\vec n=\nabla f(\vec p)=\left(\frac{\partial f(\vec p)}{\partial x},\frac{\partial f(\vec p)}{\partial y},\frac{\partial f(\vec p)}{\partial z}\right)$，指向 $f(\vec p)>0$ 的一侧
隐式平面：$(\vec p-\vec a)\cdot\vec n=0$（点法式），将 $\vec n$ 取代为平面内的两个向量叉乘后得到隐式方程 $(\vec p-\vec a)\cdot((\vec b-\vec a)\times(\vec c-\vec a))=0$ （三点求平面），将这个式子表示成行列式：
$$ \left|\begin{matrix} x-x_a & y-y_a & z-z_a \\ x_b-x_a & y_b-y_a & z_b-z_a \\ x_c-x_a & y_c-y_a & z_c-z_a \\ \end{matrix}\right|=0 $$3D 二次曲面：球体可以写成 $f(\vec p)=(\vec p-\vec c)-r^2$，椭圆球。
从隐式曲面得到三维曲面：两个曲面的交线
2D 参数曲线：$\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}g(t)\\f(t)\end{bmatrix}$，写成向量形式为 $\vec p=f(t)$
2D 参数直线：$\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}x_0+t(x_1-x_0)\\y_0+t(y_1-y_0)\end{bmatrix}$，向量形式为 $\vec p(t)=\vec {p_0}+t(\vec {p_1}-\vec {p_0})$，也可以写成 $\vec p(t)=\vec {o}+t\vec d$（源点和距离向量），当 $\vec d$ 为单位向量时，这个曲线是被弧长参数化的（不理解这个概念）
2D 参数圆：$\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}x_c+r\cos\phi\\y_c+r\sin\phi\end{bmatrix}$（$\phi$ 的取值范围为任意一个长度为 $\pi$ 的半开区间，如 $(0,2\pi]$），椭圆曲线即 $\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}x_c+a\cos\phi\\y_c+b\sin\phi\end{bmatrix}$。
3D 参数曲线：$\begin{bmatrix}x\\y\\z\end{bmatrix}=\vec p(t)$
3D 参数直线：$\vec p=\vec o+t\vec d$
3D 参数曲面：$\begin{bmatrix}x\\y\\z\end{bmatrix}=\vec p(u, v)$，例如球的表达式为 $\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}r\cos\phi\sin\theta\\r\sin\phi\sin\theta\\r\cos\theta\end{bmatrix}$。固定一个参数的形成的曲线称为等参曲线（如 $\vec q(t)=\vec p(t, v_0)$ 固定 $v$ 为 $v_0$），等参曲线 $\vec q(t)$ 对 $t$ 的导函数 $\vec{q}^{'}(t)$ 描述了切线，把它记作 $\vec {p_u}$，把固定 $u$ 的曲线导数记作 $\vec{p_v}$，可得 法向量 $\vec u=\vec{p_u}\times\vec{p_v}$，规定这个方向为外侧
总结：
- 隐式曲线、隐式曲面：$f:\mathbb R^2\mapsto\mathbb{R}$ 或 $f:\mathbb R^3\mapsto\mathbb{R}$，$S=\{\vec p|f(\vec p)=0\}$，梯度给出法向量，切向量由前面构造正交基的方法得到
- 2D 和 3D 参数曲线：$\vec p:D\subset \mathbb R\mapsto\mathbb{R}^2$ 或 $\vec p:D\subset \mathbb R\mapsto\mathbb{R}^3$，$S=\{\vec p(t)|t\in D\}$，导函数给出切向量，法向量由前面构造正交基的方法得到
- 参数曲面：$\vec p:D\subset \mathbb R^2\mapsto \mathbb R^3$，$S=\{\vec p(u,v)|(u,v)\in D\}$，导函数给出切向量，法向量由前面构造正交基的方法得到
- 3D 直线没有隐式的形式
线性插值
线性插值：$\vec p=(1-t)\vec a+t\vec b$，其中 $t\in[0,1]$
一组位置 $(x_0,y_0),(x_1,y_1),...,(x_n,y_n)$ 的线性插值：之间通过直线相连，参数 $t=\frac{x-x_i}{x_{i-1}-x_i}$，得到 $f(x)=y_i+\frac{x-x_i}{x_{i-1}-x_i}(y_{i+1}-y_i)$
三角形
三角形是图元的基础，颜色等信息会标记到三角形顶点上，重心坐标系
2D 三角形
2D 三角形面积（顺时针为负号，逆时针为正号）：
$$ A =\frac{1}{2} \left|\begin{matrix} x_b-x_a & x_c-x_a \\ y_b-y_a & y_c-y_a \\ \end{matrix}\right| $$重心坐标系：把点 $A$ 当做原点，$\overrightarrow {AB}$ 和 $\overrightarrow {AC}$ 当做（非正交）基构建的坐标系。在这个坐标系中，任何点都可以写成：
$$ \vec p=\vec a+\beta(\vec b-\vec a)+\gamma(\vec c -\vec a) $$可以展开：
$$ \vec p=(1-\beta-\gamma)\vec a+\beta\vec b+\gamma\vec c $$人们通常会令 $\alpha=1-\beta-\gamma$ 从而写成一个对称的形式：
$$ \vec p(\alpha,\beta,\gamma)=\alpha\vec a+\beta\vec b+\gamma\vec c $$这个重心坐标系有一个好处，就是：
- 当 $\alpha$、$\beta$、$\gamma$ 都在 $(0,1)$ 范围内时，点 $\vec p$ 位于三角形内部（不包括边）
- 当 $\alpha$、$\beta$、$\gamma$ 其中一个为 $0$，另外两个在 $(0,1)$ 范围内时，点 $\vec p$ 位于三角形的边上（不包括顶点）
- 当 $\alpha$、$\beta$、$\gamma$ 其中两个为 $0$，其余一个为 $1$ 时，点 $\vec p$ 位于三角形的顶点上
笛卡尔坐标系转换到重心坐标系：
作平行线，例如对于 $\beta$ 来说，作 $AC$ 这条边的平行线，过 $A$ 点的平行线 $\beta=0$，过 $B$ 点的平行线 $\beta=1$，在某条平行线上的点的 $\beta$ 值相等，并且 $\beta$ 与该距离成正比关系，所以：
$$ \beta=\frac{f_{ac}(x,y)}{f_{ac}(x_b,y_b)}=\frac{(y_b-y_a)x+(x_b-x_a)y+x_ay_b-x_by_a}{(y_b-y_a)x_b+(x_b-x_a)y_b+x_ay_b-x_by_a} $$同理：
$$ \gamma=\frac{f_{ab}(x,y)}{f_{ab}(x_c,y_c)}=\frac{(y_c-y_a)x+(x_c-x_a)y+x_ay_c-x_cy_a}{(y_c-y_a)x_c+(x_c-x_a)y_c+x_ay_c-x_cy_a} $$然后：
$$ \alpha=1-\beta-\gamma $$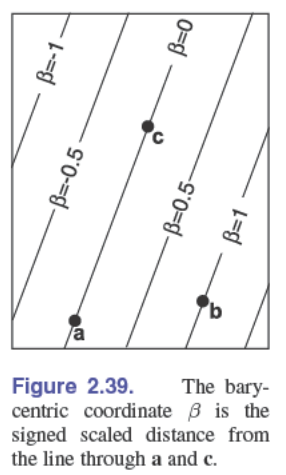
一个更简洁的计算方式是用面积，底相同，高（距离）与面积成比例：
$$ \alpha=A_a/A\\ \beta=A_b/A\\ \gamma=A_c/A $$
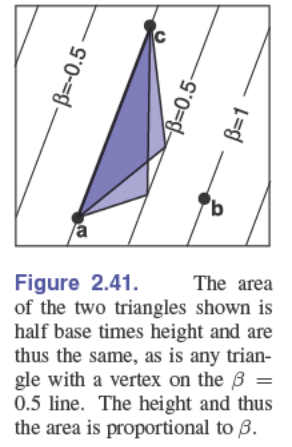
可以发现：
$$ A_a+A_b+A_c=A $$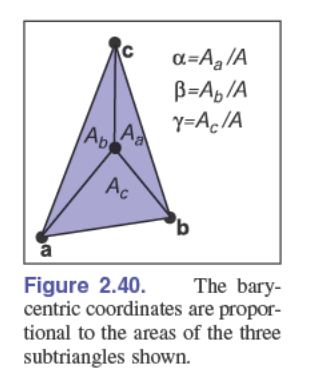
3D 三角形
2D 可以完美延伸到 3D，所以仍然使用：
$$ \vec p(\alpha,\beta,\gamma)=\alpha\vec a+\beta\vec b+\gamma\vec c\\ \alpha=1-\beta-\gamma $$除此之外，法向量可以由叉积得到：
$$ \vec n=(\vec b-\vec a)\times(\vec c-\vec a) $$三角形的面积可以由叉积的长度来计算：
$$ A=\frac{1}{2}\Vert (\vec b-\vec a)\times(\vec c-\vec a)\Vert =\frac{1}{2}\Vert \vec n\Vert $$既然如此，上面我们知道了 $A_a$、$A_b$、$A_c$、$A$ 与 $\alpha$、$\beta$、$\gamma$ 的关系，我们可以计算出各自的面积：
$$ A=\frac{1}{2}\Vert \vec n\Vert \\ A_a=\frac{1}{2}\Vert \vec {n_a}\Vert \\ A_b=\frac{1}{2}\Vert \vec {n_b}\Vert \\ A_c=\frac{1}{2}\Vert \vec {n_c}\Vert $$其中：
$$ \vec {n_a}=(\vec c-\vec b)\times(\vec p-\vec b)\\ \vec {n_b}=(\vec a-\vec c)\times(\vec p-\vec c)\\ \vec {n_c}=(\vec b-\vec a)\times(\vec p-\vec a)\\ $$那么：
$$ \alpha=\frac{\Vert \vec {n_a}\Vert }{\Vert \vec n\Vert }\\ \beta=\frac{\Vert \vec {n_b}\Vert }{\Vert \vec n\Vert }\\ \gamma=\frac{\Vert \vec {n_c}\Vert }{\Vert \vec n\Vert } $$考虑到 $\vec a\cdot \vec b=\Vert \vec a\Vert\Vert \vec b\Vert \cos \phi$，而根据向量同向还是反向，$\cos\phi$ 取值为 $\pm 1$，可以扩展到三角形外的情况：
$$ \alpha=\frac{\vec n\cdot \vec {n_a}}{\Vert \vec n\Vert^2 }\\ \beta=\frac{\vec n\cdot \vec {n_b}}{\Vert \vec n\Vert^2 }\\ \gamma=\frac{\vec n\cdot \vec {n_c}}{\Vert \vec n\Vert^2 } $$概率
随机变量、期望
方差：$V(X)=E((X-E(X))^2)=E(X^2)-E(X)^2$
期望与方差的运算
标准差
连续随机变量取任何特定值的概率为零
概率密度函数（Probability Density Function）
蒙特卡罗积分
使用随机数进行数值积分
$$ \int_Df(x)\mathrm{d}x=\overline{f(x)}\times\int_D 1\mathrm{d}x $$所以一般是求平均值，然后乘上一个常数
重要性采样：当函数的高值和低值变化很大时，将样本集中在某些区域，然后用权值校正不均匀性。使用概率密度函数
具体流程为：
- 确定采样的函数与定义域
- 确定一个随机生成采样点的算法，同时确定采样点的概率密度函数
- 计算 ${f(x_i)}/{p(x_i)}$ 的均值
练习
- 浮点数的基数是无穷
- 可以实现 32 到 64，让它有明确的逆，但不是所有函数都可逆
- $C=\{(x,y,z)|x,y,z\in[0,1]\}$
- $\log_bx=\frac{\ln x}{\ln b}$，如果 $b$ 是负数，那么根据 IEEE，应该返回 NaN
- $x^3+3x+2=0$，$x=\frac{-3\pm\sqrt{3^2-4\times 2}}{2}=-1/-2$
- 代码如下：
if a == 0:
if b == 0:
return 0
else:
x1 = -c / b
return 1, x1
else:
delta = b * b - 4 * a * c
if delta < 0:
return 0
elif delta == 0:
x1 = -b / (2 * a)
return 1, x1
else:
x1 = (-b + sqrt(delta)) / (2 * a)
x2 = (-b + sqrt(delta)) / (2 * a)
if x1 > x2:
x1, x2 = x2, x1
return 2, x1, x2
- 略
- 略
- $\vec u=\frac{\vec a}{\Vert\vec a\Vert}$，$\vec w=\frac{\vec u \times\vec b}{\Vert\vec u \times\vec b\Vert}$，$\vec v=\vec w \times\vec u$
- $(2x,1,9z)$
- $\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}x_c+a\cos\phi\\y_c+b\sin\phi\end{bmatrix}$
- $x+y+z-1=0$（点法式推导），$\vec p(u,v)=(1,0,0)+u(-1,1,0)+v(-1,0,1)$（实际上是重心坐标系），$(1,1,1)$（叉乘即可）
- 分为以下几步（https://cloud.tencent.com/developer/article/2313839）：
- 计算四个叉乘：$d_1=\overrightarrow{a_0b_0}\times\overrightarrow{b_0a_1}$、$d_2=\overrightarrow{a_0b_1}\times\overrightarrow{b_1a_1}$、$d_3=\overrightarrow{b_0a_0}\times\overrightarrow{a_0b_1}$、$d_4=\overrightarrow{b_0a_1}\times\overrightarrow{a_1b_1}$
- 如果 $d_1\cdot d_2<0$（$b_0$ 与 $b_1$ 在 $\overrightarrow{a_0a_1}$ 两侧）且 $d_3\cdot d_4<0$（$a_0$ 与 $a_1$ 在 $\overrightarrow{b_0b_1}$ 两侧），那么相交
- 对于 $d_1$ 到 $d_4$，如果存在一个 $d_i=0$ 且对应的点在线段内部，那么相交
- 上面的情况都不满足则不相交
- 前面说的笛卡尔坐标系转重心坐标系就行
- 略