大多数计算机图像以某种“光栅显示(raster display)”的形式呈现给用户
光栅显示器将图像显示为矩形像素(pixel)阵列
由于光栅显示非常普遍,所以光栅图像(raster image)是存储和处理图像的常用方法,即一个二维数组,通常存储 RGB 三个颜色作为像素值(pixel value)
显示的像素与图像的像素通常不相同,最好将光栅图像视为与设备无关的数据结构
矢量图片(vector image)是存储形状描述的数据结构
光栅设备
光栅设备可以分类为:
- 输出设备:
- 显示设备:
- 透射式:液晶显示器(LCD)
- 放射式:发光二极管显示器(LED)
- 硬拷贝设备:
- 二进制:喷墨打印机
- 连续色调:热升华打印机
- 显示设备:
- 输入设备:
- 2D 阵列传感器:数码相机
- 1D 阵列传感器:平板扫描仪
透射式显示器:像素本身不发光,而是通过改变允许通过的光源,依赖显示器的光源。液晶显示器(LCD)通过改变电压来控制液晶的旋转,从而改变偏振光
放射式显示器:使用直接发射可控光亮的像素。发光二极管显示器(LED)由半导体期间组成,通过控制电流来控制半导体器件的发光强度
打印机也是像显示器一样的光栅设备
二进制打印:喷墨打印机,颜料只会留在应该接收墨水的网格位置,彩色打印通过比例混合不同颜色的颜料实现
连续色调打印:热升华打印机,每个像素处沉积不同量的染料,加热来控制染料的扩散,所以能产生连续的颜色范围
打印机分辨率由“像素密度(pixel density)”来描述,而不是总像素数量,通常单位是 ppi(pixel per inch)和 dpi(dots per inch),分别用在连续色调打印机和二进制打印机中。
因为二者原理不同,二进制打印机需要更精密的网格
2D 阵列传感器:数码相机使用光敏像素网格,滤色器阵列来让每个像素只能看到红色、绿色或者蓝色的光,图像处理软件来填充缺失的值。其他相机使用三个单独阵列
1D 阵列传感器:滤光片,测量三种颜色时有适当的延迟,所以可以进行独立的颜色测量,单位 ppi
图像、像素和几何
图像可以被抽象为一个函数:
$$ I(x,y):R\mapsto V $$其中,$R\subset \mathbb R^2$ 是一个矩形区域,$V$ 是可能的像素值的集合,$V$ 可以是 $\mathbb R^+$(灰度图像)、$(\mathbb R^+)^3$(可以是 RGB)等
光栅图像中的像素是连续图像这个点附近的平均颜色的测量
像素在 2D 空间中的分布:
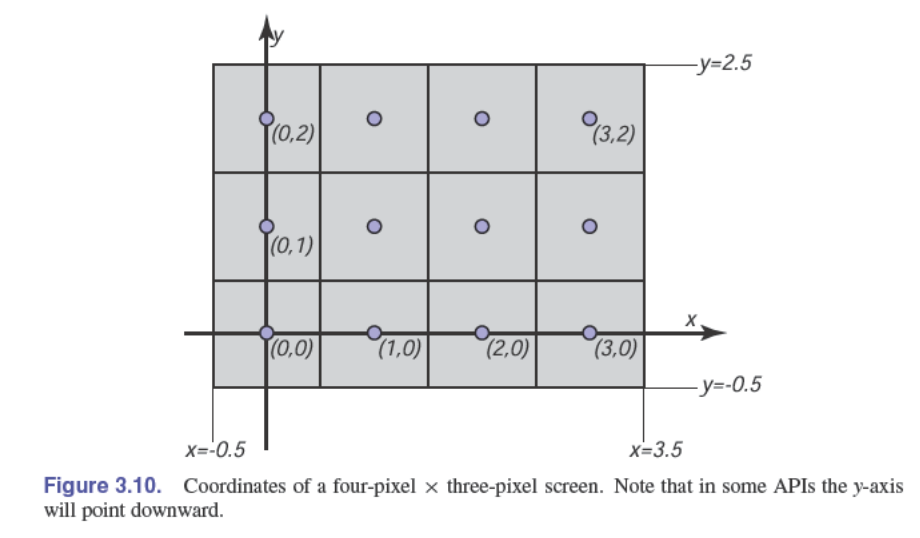
一些常用的像素格式:
- 1-bit 灰度
- 8-bit RGB 固定范围色彩(共 24-bit):消费级照片
- 8-bit 到 10-bit RGB 固定范围色彩(共 24-bit 到 30-bit):电脑的数字界面
- 12-bit 到 14-bit RGB 固定范围色彩(共 36-bit 到 42-bit):RAW 图像
- 16-bit RGB 固定范围色彩(共 48-bit):专业摄像机和打印机
- 16-bit 固定范围灰度(共 48-bit):放射学和医学成像
- 16-bit 半精度浮点 RGB:HDR 图像,用于实时渲染的中间格式
- 32-bit 浮点 RGB:用于 HDR 图像的软件渲染和处理的通用中间格式
人为引入的伪影:裁剪到最大值、四舍五入时产生的伪影
Gamma 校正:显示器对光强变化的响应通常不是线性的(比如:明明图像上某个像素的强度是 $0.5$ 个最大强度,显示在显示器上变成 $0.25$ 个最大强度),通常会出现这样的关系:
$$ \text {显示强度}=\text {最大强度}\times a^\gamma $$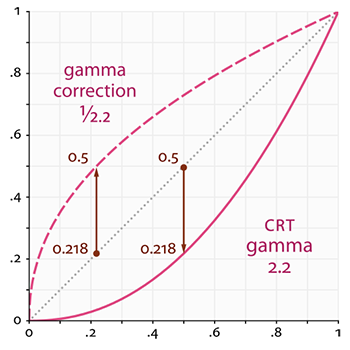
通过 Gamma 校正可以让它再近似回到线性,取强度为 $0.5$,那么有:
$$ 0.5=a^\gamma $$如果我们找到了 $a$,我们就能推导出 $\gamma$ 的值:
$$ \gamma=\frac{\ln 0.5}{\ln a} $$在很多游戏中,第一次进入它会让我们调整到刚好能看清的亮度,这就是在寻找 $a$ 的值。
在得到 $\gamma$ 之后,我们就可以执行 Gamma 校正了,在 Gamma 校正后,强度从 $a$ 变成 $a'$,有:
$$ \text {显示强度}=\text{最大强度}\times(a')^\gamma $$显然,我们只需要让:
$$ a'=a^{\frac{1}{\gamma}} $$就能得到线性的效果了。
真实显示器的另一个重要特征是使用量化的值,虽然中间格式是浮点,但是传给显示器的通常是整数(通常是 0-255),这意味着 $a$ 的取值为:
$$ a\in\left\{\frac{0}{255},\frac{1}{255},\ldots,\frac{255}{255}\right\} $$显示器显示出来的强度为:
$$ \left\{M\left(\frac{0}{255}\right)^\gamma,M\left(\frac{1}{255}\right)^\gamma,\ldots,M\left(\frac{255}{255}\right)^\gamma\right\} $$其中,$M$ 是最大强度
RGB 颜色
大多数计算机图形图像是用 RGB 颜色定义的
RGB 将三种颜色以相加的方式混合
以 RGB 为坐标轴,所有色彩都能表示
常见:
| 颜色 | R | G | B |
|---|---|---|---|
| 黑色 Black | 0 | 0 | 0 |
| 红色 Red | 1 | 0 | 0 |
| 绿色 Green | 0 | 1 | 0 |
| 蓝色 Blue | 0 | 0 | 1 |
| 黄色 Yellow | 1 | 1 | 0 |
| 品红色 Magenta | 1 | 0 | 1 |
| 青色 Cyan | 0 | 1 | 1 |
| 白色 White | 1 | 1 | 1 |
Alpha 合成
部分覆盖像素的内容
Alpha 通道
像素覆盖率称为 $\alpha$,有:
$$ \vec c=\alpha\vec {c_f}+(1-\alpha)\vec{c_b} $$这是前景色 $\vec {c_f}$ 和背景色 $\vec{c_b}$ 的一个插值,当 $\alpha=1$ 时完全不透明,当 $\alpha=0$ 时完全透明
图像存储
原始存储太大,通常进行压缩(有损或无损),通常有 jpeg、tiff、ppm、png 等格式,无需细究