图形学的基本任务之一是渲染三维对象，以一组对象为输入，以像素数组为输出

可以分为两个大概的方法：对象顺序渲染（object-order rendering，对每个对象找到影响的像素并更新）和图像顺序渲染（image-order rendering，对每个像素找到对应的对象并更新）

对象顺序渲染和图像顺序渲染计算出的结果相同，但适合不同任务，拥有不同的性能特征。广义上讲图像顺序渲染容易产生更灵活的效果，但需要更多的执行时间

光线追踪（Ray tracing）是一个图像顺序渲染算法

基础的光线追踪算法

一次计算一个像素，对于每个像素，找到对应的位置能够看到的对象。

观察射线（viewing ray）：一条从视点（viewpoint）发射出来的朝向像素观察方向的射线

任何被像素“看”到的物体都应该与观察射线相交，我们想要的特定对象时距离摄像机最近的与观察射线相交的对象，因为它会阻挡后面任何其他对象

找到对象后，着色计算器（shading computation）会使用交点、表面法线和其他信息来确定像素的颜色

基本的光线追踪器有三个部分：

• 射线生成（ray generation）：计算每个像素观察射线的原点和方向
• 射线相交（ray intersection）：找到最近的与观察射线相交的对象
• 着色（shading）：根据射线相交的结果计算像素颜色

视角（Perspective）

艺术家尝试过很多使用二维绘画表现三维物体的方法，其中有很多非传统的方法，包括立体派绘画、鱼眼镜头、外围相机，但标准方法是线性透视

线性透视（linear perspective）：三维对象被投影（project）到一个图像平面（image plane）上，在这个过程中场景中的直线成为图像中的直线

平行投影（parallel projection）：沿着投影方向（projection direction）移动三维中的点，把它们放到图像上。投影的效果与投影方向和图像平面的选择有关。如果图像平面垂直于投影方向，那么称它是正交（orthographic）投影，否则称它是斜（oblique）投影。它常用于机械和建筑图形，因为它可以保留图像的大小和形状。同时这也是它的局限性，与日常生活经验不同，呈现处理的对象大小与远近无关。

透视投影（perspective projection）：沿着经过视点的射线而不是平行线投影。这样保证距离视点较远的对象在投影时会变小。投影的效果与视点和图像平面决定。视点在图像中心后面的称为非倾斜投影，否则就是斜投影

三点透视（three-point perspective）：看不懂，对应的还有一点透视和两点透视

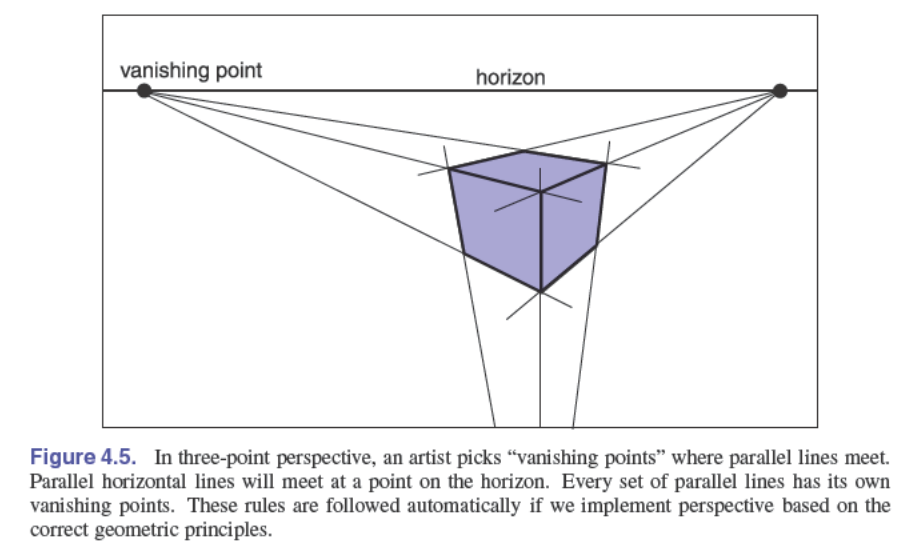
计算观察射线

射线的数学表示：

原点 $\vec e$ 沿着 $(\vec s-\vec e)$ 方向的射线，当 $t<0$ 时，点 $\vec p(t)$ 在原点“后面”

所有的射线生成方法都是在一个叫做相机坐标系（camera frame）的正交坐标系开始的，这个坐标系长这样：

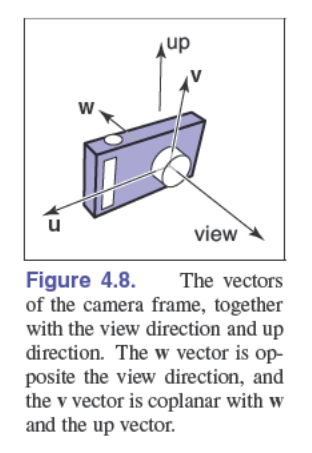
其中，原点（视点）我们称之为 $\vec e$，即 eye

不管是平行投影还是透视投影，都可以用相机坐标系来表示，如下：

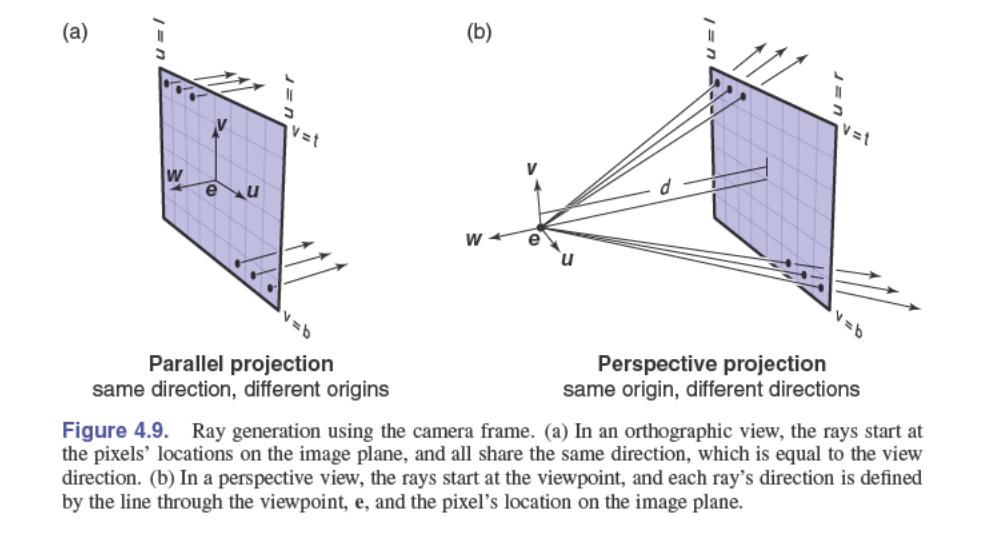
除了坐标系原点 $\vec e$ 之外，使用 $l$、$r$、$t$、$b$ 一起约束了图像的尺寸和位置。

为了将 $n_x\times n_y$ 个像素匹配到大小为 $(r-l)\times (t-b)$ 的矩形上，我们可以计算一下每个像素在矩形中的位置，对于 $(i,j)$ 这个像素来说，位置为：

知道了每个像素对应的位置，我们可以得到两种投影方式的射线：

一个射线类：

class Ray
    Vec3 o
    Vec3 d
    Vec3 evaluate(real t)
        return o + td

射线与物体的交点

在生成了观察射线之后，我们需要找到这个射线与物体的第一个交点

射线与球面交点

球面通常使用隐式曲面表示，即给一个 $f(\vec p)=0$，此时我们只需要代入 $\vec p(t)=\vec e+t\vec d$：

球面的隐式方程为：

代入后：

这是个二次方程，直接解即可。另外，交点 $\vec p$ 处的法向量为 $\vec n=2(\vec p-\vec c)$，单位法向量为 $(\vec p-\vec c)/r$

射线与三角的交点

有许多算法，这里介绍重心坐标表示的参数平面，因为它除了三角形的顶点之外不需要长期存储（？）

参数平面为 $\vec f(u,v)$，或者写成 $\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}f_x(u,v)\\f_y(u,v)\\f_z(u,v)\end{bmatrix}$，我们直接代入 $\vec p(t)=\vec e+t\vec d$ 即可：

对于三角形重心坐标系来说，它的参数方程为：

代入：

我们可与把它展开：

写成矩阵形式：

然后使用克莱默法则求解：

其中：

三阶行列式可以展开来计算，可以使用“ei-minus-hf”的方式减少操作数量

boolean raytri(Ray r, vec3 a, vec3 b, vec3 c, interval [t0, t1])
    compute t
    if (t < t0) or (t > t1) then
        return false
    
    compute gamma
    if (gamma < 0) or (gamma > 1) then
        return false
    
    compute beta
    if (beta < 0) or (beta > 1 - gamma) then
        return false
    
    return true

软件中的射线求交

面向对象是个好主意

class HitRecord
	Surface s
	real t
	Vec3 n

class Surface
	HitRecord hit(Ray r, real t0, real t1)

Surface 是一个基类，派生 Triangle、Sphere 等子类

与一组对象相交

作为 Surface 的一个子类

class Group : Surface
    list-of-Surface surfaces
    HitRecord hit(Ray r, real t0, real t1)
    	HitRecord closet-hit(inf)
        for surf in surfaces do
            rec = surf.hit(ray, t0, t1)
            if rec.t < inf then
                closest-hit = rec
                t1 = t
        return closest-hit

注意 t1 = t 这句话可以不断缩小求交的范围，所以最后一定是更近的

着色（Shading）

我们已经知道了一个像素的可见表面，那么像素值可以通过着色模型（shading model）计算得出。

如何实现着色模型取决于应用程序，从简单的启发式到复杂的基于物理的模型都有，之后会讨论

事实上，一个着色模型既可以被用于光线追踪，也可以被用于对象顺序渲染

光源

着色模型支持基本的三种类型的点光源：

• 点光源（point light）：从空间中的一点发出光线
• 定向光源（directional light）：从单一方向照亮场景
• 环境照明（ambient light）：提供恒定的照明以填充阴影

更高级的还支持：

• 区域光源（area light）：发光的场景几何体
• 环境光源（environment light）：使用图像来表示来自遥远来源的光

计算点光源、定向光源的着色需要四种向量：

• 着色点的位置 $\vec x$，使用 ray tracing 计算得到
• 表面法线 $\vec n$，使用 ray tracing 计算得到，或者也可以直接计算
• 光线方向 $\vec l$，根据光源计算得到
• 朝向方向（viewing direction） $\vec v$，指的是反射光朝向的方向，是射线的反方向，即 $\vec v=-\frac{\vec d}{\Vert\vec d\Vert}$

来自环境照明的着色更简单：没有 $\vec l$ 因为光来自四面八方，并且着色也不取决于朝向方向 $\vec v$。有时甚至不依赖于 $\vec x$ 和 $\vec n$

在包含多个光源的场景下，着色只是简单地将灯光的贡献加起来

软件中的着色

光源与材质，光源是 Light 类，存有足够的信息来描述光源，材质是 Material 类，封装了一切着色模型计算需要的东西

不同的系统使用不同的方法将光线和材质的职责分开，本章让光线负责整体的照明计算，而让材质负责计算 BRDF 值，如下：

class Light
    Color illuminate(Ray ray, HitRecord hrec)

class Material
    Color evaluate(Vec3 l, Vec3 v, Vec3 n)

每一个 Surface 都存储一个对自身 Material 的引用

一个点光源可以写成：

class PointLight : Light
    Color I // 点光源颜色
    Vec3 p // 点光源位置
    Color illuminate(Ray ray, HitRecord hrec)
        Vec3 x = ray.evaluate(hrec.t) // 得到位置
        real r = || p - x || // 光源距离表面的距离 
        Vec3 l = (p - x) / r // 入射光线方向向量
        Vec3 n = hrec.n  // 表面法线
        Color E = max(0, dot(n, l)) * I / r ^ 2 // 这里应该第 5 章会讲，计算出颜色
        Color k = hrec.surface.material.evaluate(l, v, n) // 应该第 5 章会讲
        return kE

一个环境照明可以写成（环境系数是材质的属性）：

class AmbientLight : Light
    Color Ia // 环境光照颜色
    Color illuminate(Ray ray, HitRecord hrec)
        Color ka = hrec.surface.material.ka
        return ka * Ia // 环境光照颜色乘上环境光照系数

完整计算，包括求交及处理多个光源：

void shade-ray(Ray ray, real t0, real t1)
    HitRecord rec = scene.hit(ray, t0, t1)
    if rec.t < inf then // 有相交的对象
        Color c = 0
        for light in scene.lights do
            c = c + light.illuminate(ray, rec)
        return c
    else
        return background-color

这种设置将材质和光源分开，并且允许透明地（指实现对调用者透明）添加新的材质和光线。纹理添加了复杂性

没有体现与其他对象的关系（这里指的是下面的阴影）

阴影（Shadows）

阴影射线（shadow ray）：决定是否在阴影中的射线，从某个位置 $\vec x$ 指向光源，与前面的观察射线不同（观察射线的方向由透视方式决定，而不取决于环境中的对象或光源）

阴影射线表示为 $\vec x+t\vec l$，$\vec l$ 表示方向

若光源处 $t_1=r$，那么如果 hit 到的物体 $t\in[0,r]$，那么说明在阴影中。不过因为精度问题一般不取 $0$，而是取 $\epsilon$ 这样一个极小值

实现大概像这样，在代码中添加一个 if 语句：

HitRecord srec = scene.hit(Ray(x, l), epsilon, r)
if srec.t < inf then
    proceed with normal illumination calucation
else
    return 0

定向光源类似，只不过 $t_1=\infty$

每个灯光的照明计算需要单独的阴影射线，并且在计算环境光阴影时没有阴影测试。阴影在显示附近对象之间的关系方面发挥着重要的视觉作用。

镜面反射（Mirror Reflection）

在光线追踪程序中添加理想镜面反射（ideal specular reflection）或镜面反射很简单。

设入射光线方向为 $\vec d$，法线为 $\vec n$，利用入射光线在法线上的投影可以算出射光线：

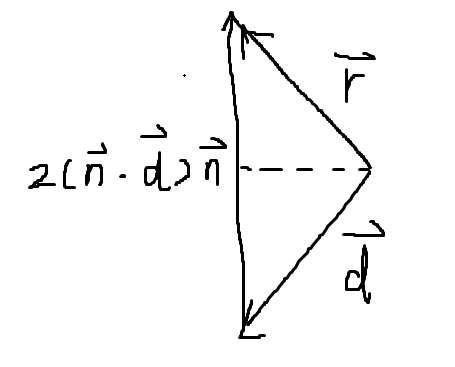
在真实世界中，反射有能量损失，这种损失对于不同颜色可能不同（例如，黄金反射黄色比蓝色反射得更多），因此它会改变所反射对象的颜色。

这可以通过在 shade-ray 中添加递归调用来实现，在计算完所有灯光的贡献后再添加一个贡献：

c = c + Km * shade-ray(Ray(p, r), 0, inf)

其中，Km 是镜面反射的 RGB 颜色，p 由是 hit 得到的位置，r 是反射光方向（对于光线来说实际上是入射光）

这句话的意思就是计算反射的光

上面递归调用的问题是它可能永远不会终止。这可以通过添加最大递归深度来修复。只有在 Km 不为零的情况下才能生成反射光线，代码将更有效。

在现实生活中，不同角度的 Km 有很大的变化

问题和练习

光线追踪通常用于拾取，即按下 F 键后让系统知道需要拾取那个物体

1. 射线 $(1, 1, 1)+t(−1, −1, −1)$ 与以原点为中心、半径为 1 的球体的交点的射线参数是什么？注意：这是一个很好的调试案例
2. 当射线 $(1, 1, 1) + t(−1, −1, −1)$ 射向顶点为 $(1, 0, 0)$、$(0, 1, 0)$ 和 $(0, 0, 1)$ 的三角形时，重心坐标和射线参数是多少？注意：这是一个很好的调试案例。
3. 略

都不想做，它说是个很好的调试案例，没准之后会用得上