光线追踪和光栅化是不同的东西
在物理世界中,我们看到的大部分光都是反射光,这种反射可以让我们建立起对形状的理解。
在计算机图形学中,着色(shading)的目的是为视觉系统提供一些对形状的线索:
- 计算机辅助设计或科学可视化中,重点是清晰度,提供清晰准确的 3D 形状
- 视觉效果和广告中,目标是最大化渲染与真实对象外观的相似性
- 动画、虚拟现实或游戏中,目标介于艺术和写实之间
着色模型、近似,从简单的开始
点状光源(Point-like Light Source)
与点光源不同,点状光源包括两种:
- 点光源(point source):光源足够小,但靠近场景,对于不同的表面有不同的照明方式
- 方向光源(directional source):大小相对于距离而言很小,可以被视为点状,同时它距离很远,所以对于所有的表面有相同的照明方式
这两个在之后计算时有一些共性,所以分成了一类
点光源由位置、强度来描述。
点光源可以是各向同性(isotropic)的,即各个方向的强度相同;也可以是各项异性的,例如很多系统中提供的点灯(spot light),只向某些特定方向发射光
对于各项同性的点光源,很容易根据能量计算出特定距离的亮度
辐照度(irradiance):电磁辐射射于表面时每单位面积的功率
对于一个功率为 $P$ 的光源,它均匀地向各个方向射出光,如果接收的球面半径为 $r$,那么辐照度 $I_r$ 应该是:
$$ I_r=\frac{P}{4\pi r^2} $$如果我们把单位圆处的辐照度记为 $I$,那么:
$$ I_r=\frac{I}{r^2} $$在图形学中,我们把单位圆处的辐照度 $I=P/(4\pi)$ 看做光源的强度,$r^{-2}$ 这个平方反比项描述了辐照度如何依赖于光源到表面的距离 $r$
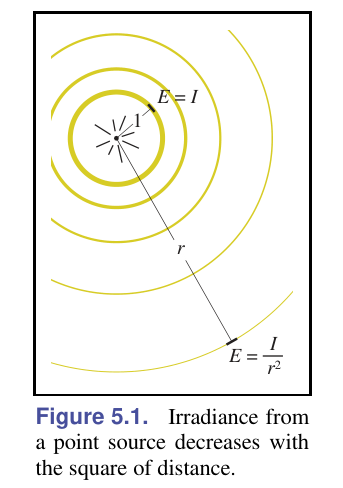
其实我们上面得到的是球面的辐照度,球面的法线总是指向球心
在具体的表面上,一个重要的因素是入射角(angle of incidence,表面法线入射光线的夹角),根据兰伯特余弦定律(Lambert’s cosine law),辐照度与入射角有这样的关系:
$$ I_r=I\frac{\cos\theta}{r^2} $$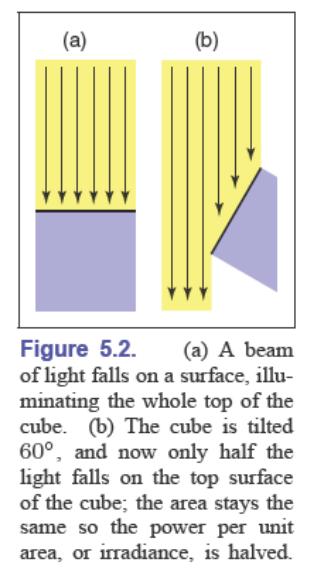
当我们选择一个很小的表面时,外部光线就是平行光。
根据辐照度的定义,在一个微小表面上,我们如果进行旋转,会发现照射到表面的总光线减少了,但是面积不变,这样就能大致理解这个定律的含义了
其中 $\cos\theta$ 可以由点乘表示:
$$ \cos\theta=\vec n\cdot \vec l $$其中 $\vec n$ 是表面法线,$\vec l$ 是指向光源的向量
方向光是点光源的极限,此时所有表面都是“微小表面”,所以 $r^{-2}$ 几乎不变,我们把 $\frac{I}{r^2}$ 看成常量 $H$,那么有:
$$ I_r=H\cos\theta $$基础反射模型(Reflection Model)
前面我们计算了辐照度,它描述了光线照射到物体上的情况,接下来就看如何反射光线
在这一章,作者使用了简单的模型,不考虑次表面反射这种,仅仅有一个 base layer(提供基础颜色)和一个 surface(反射)
朗伯反射(Lambertian Reflection)
最简单的就是平等地反射光到所有方向,而不管它来自哪里,仅仅乘个反射系数即可:
$$ L_r=kI_r $$这种表面被称作理想漫反射表面(ideal diffuse surface),颜色是独立于视角的(view independent),完全取决于反射率(reflectance)$R$,可以写成(原因之后章节会讲):
$$ L_r=\frac{R}{\pi}I_r $$对于不同颜色的光,反射率可能不同,可能会有 3 个不同的反照率对应不同的通道。
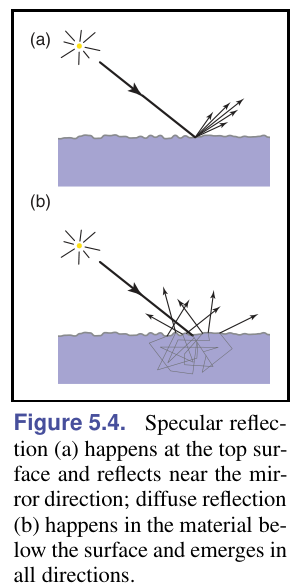
在物理上,朗伯反射描绘了这样一种情况:在一个平坦的、粗糙的表面上,光会在材料内部反射,以至于“忘记”了自己从哪里来,并随机地向各个方向射出
镜面反射(Specular Reflection)
颜色与视点有关
理想镜面反射(ideal specular reflection):入射光只朝一个方向反射
光泽反射(glossy reflection):表面并非完全光滑
Blinn–Phong 模型、改进的 Blinn–Phong 模型
镜面反射可以看成是反射光方向向量 $\vec v$、单位法线向量 $\vec n$、入射光的反方向向量 $\vec l$ 的函数。理念是当 $\vec v$ 与 $\vec l$ 对称时最亮,并且当非对称时,光亮可以平滑地变化
用半程向量(half vector)来描述与“镜面配置”的距离,用 $\vec h$ 来表示:
$$ \vec h=\frac {\vec l+\vec v}{\Vert\vec l+\vec v\Vert} $$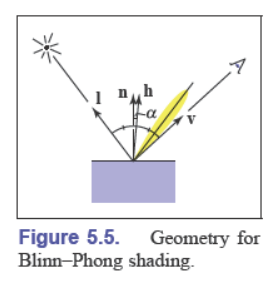
我们使用 $\vec n$ 与 $\vec h$ 的点积来测量他们的近似度(实际上就是余弦值),为了让它变化更快,取 $p$ 次幂,$p$ 被称作 Phong 指数即
$$ (\vec n\cdot\vec h)^p $$把这个东西变成个系数,然后再加上漫反射,就能得到:
$$ L_r=\left(\frac{R}{\pi}+k_s\max(0,\vec n\cdot\vec h)^p\right)I_r $$其中,$(\vec n\cdot\vec h)^p$ 与 $0$ 取了个最大值来防止二者过于偏离。$k_s$ 是镜面反射系数(specular coefficient,三通道可以不同)来控制高光部分有多亮
这个式子中的系数被称作双向反射分布函数(bidirectional reflectance distribution function,BRDF),即:
$$ f(\vec v, \vec l,\vec n) $$对于漫反射来说,BRDF 是个常函数,对于镜面反射来说不是
着色计算可以被分为两部分,一个是计算 BRDF,另一个是计算辐照度,最后相乘
计算着色
使用上面的划分可以很容易写出干净的代码:辐照度计算仅依赖光源和表面几何,BRDF 计算仅依赖表面属性和观察几何
基本着色计算(这里指的是计算辐照度)可以在光线追踪和光栅化系统中以完全相同的方式完成,仅仅是输入不同,在光栅化系统中我们需要:
- 着色点 $\vec x$
- 表面单位法向量 $\vec n$
- 点光源的位置 $\vec p$ 或者定向光源的方向 $\vec l$
- 点光源的强度 $I$ 或者定向光源的辐射强度 $H$
首先计算 $I_r$,对于点光源,需要先计算出 $r$ 和 $\vec l$:
$$ \begin{gather*} r=\Vert\vec p-\vec x\Vert\\ \vec l=\frac{\vec p-\vec x}{r}\\ I_r=\frac{\max(0,\vec n\cdot\vec l)}{r^2}I \end{gather*} $$对于定向光源:
$$ I_r=\max(0,\vec n\cdot\vec l)H $$计算出 $I_r$ 之后,在光线追踪中,我们通过递归的方式计算反射光,但在光栅化中,我们要计算 BRDF,然后二者相乘,我们需要:
- 光源方向向量 $\vec l$
- 出射光线方向向量 $\vec v$
- 描述表面性质的参数,反照率 $R$、镜面系数 $k_s$ 和 Phong 指数 $p$
注意 $\vec v$、$\vec l$、$\vec n$ 必须是单位向量
环境照明(Ambient Illumination)
假设环境光在场景中的所有方向和所有位置都完全相同。
进一步假设环境光仅被漫反射(因为没有光线方向,因此无法计算镜面着色)。
这使得环境着色非常简单:它是一个常数!
通常,这个常数是材质相关的环境反射系数(ambient reflection coefficient) $k_a$ 和光源相关的环境强度 $I_a$ 的乘积:
$$ L_r=k_a\times I_a $$但是,物体对大型光源的反应有不同:物体的角落或者凹陷区域往往更暗
一些系统将它视作一个光源,另一些系统将它视作场景的一个参数(例如 Unity)
问题与练习
Phong 模型转向基于微表面的模型
pow() 函数在专为图形学设计的系统中较快但精度较低
直接贴 chatgpt 的答案了:


