建议看一下这个视频：https://www.bilibili.com/video/BV13e411m7Js
从二维平面平行四边形的面积入手，我们可以得到二阶行列式的三条公理：
$$ \det(\vec{u_1}+k\vec{u_2},\vec v)=\det(\vec{u_1},\vec v)+k\det(\vec{u_2},\vec v)\\ \det(\vec{u},\vec v)=\det(\vec u+k\vec v,\vec v)\\ \begin{vmatrix}1 & 0\\0 & 1\end{vmatrix}=1 $$这三个式子分别称为线性性（把一条边 $\vec u$ 拆成两条边，这两条边代表的平行四边形的面积之和就是大平行四边形的面积）、平移不变性（平行四边形的对边滑动不改变面积）、单位面积（单位正方形的面积为 $1$）
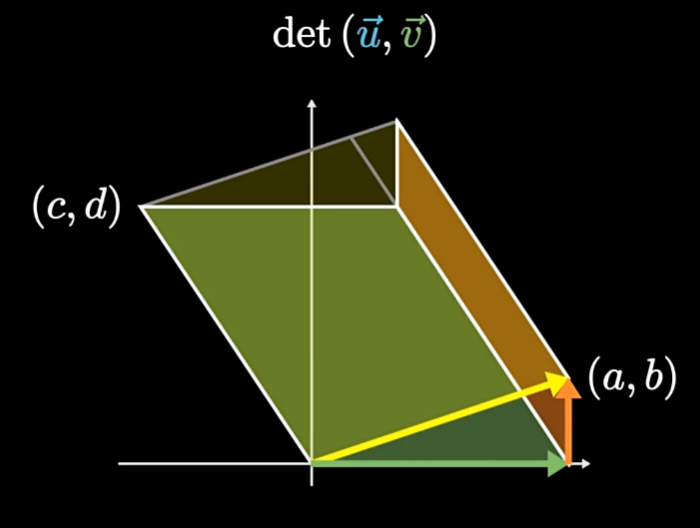
由此我们可以得到行列式的一个重要的性质：
$$ \det(\vec u, \vec v)=-\det(\vec v, \vec u) $$这叫做行列式的反对称性，对换会导致符号改变，这个性质是“有向面积”的结果
除此之外，根据面积，还有性质：
$$ \det(\vec u,\vec{u})=0 $$然后我们来看一下展开式：
$$ \begin{align} \det (\vec a,\vec b)& =\det (x_a\vec x+y_a\vec y,x_b\vec x+y_b\vec y)\\ & = x_ax_b\det (\vec x,\vec x)+x_ay_b\det (\vec x,\vec y)+y_ax_b\det (\vec y,\vec x)+y_ay_b\det (\vec y,\vec y) \\ & = x_ax_b(0)+x_ay_b(+1)+y_ax_b(-1)+y_ay_b(0) \\ & = x_ay_b-y_ax_b \end{align} $$同样，二阶行列式可以扩展到三阶：
$$ \det(\vec{u_1}+k\vec{u_2},\vec v,\vec w)=\det(\vec{u_1},\vec v,\vec w)+k\det(\vec{u_2},\vec v,\vec w)\\ \det(\vec{u},\vec v,\vec w)=\det(\vec u+k\vec v,\vec v,\vec w)\\ \begin{vmatrix}1 & 0 & 0\\0 & 1 & 0\\1 & 0 & 1\end{vmatrix}=1\\ \det(\vec u, \vec v, \vec w)=-\det(\vec v, \vec u, \vec w)=-\det(\vec u, \vec w, \vec v)=-\det(\vec w, \vec v, \vec u)\\ \det(\vec u, \vec u, \vec w)=\det(\vec u, \vec v, \vec v)=\det(\vec w, \vec v, \vec w)=0 $$这样，我们就把行列式与面积或者体积联系到了一起。
矩阵加法与乘法、转置（transpose）、逆矩阵（inverse matrix）
矩阵中的向量操作、外积（outer product，$\mathbf a\mathbf b^\mathrm{T}$）、向量积（$\mathbf a^\mathrm{T}\mathbf b$）
对角矩阵（diagonal matrix）、对称矩阵（symmetric matrix）、正交矩阵（orthogonal matrix，这里的正交矩阵指的是行向量或列向量彼此正交且长度均为 $1$）
余子式（cofactor）$a^c_{ij}$、协因数矩阵（cofactor matrix）、伴随矩阵（adjoint）$\mathbf{A}^*=[a^c_{ji}]_{n\times n}$、求逆 $\mathbf{A}^{-1}=\frac{1}{|\mathbf{A}|}\mathbf{A}^*$
线性方程组（Linear Systems）、克莱默法则（Cramer’s rule）
特征值（eigenvalues）、正交分解、（相似）对角化（iagonalization，任何实对称矩阵都可以相似对角化）
奇异矩阵（singular matrix，非满秩矩阵）
奇异值分解（Singular Value Decomposition，SVD，也就是可以整理基向量的方法）
练习：
- 用二阶行列式写一个隐式方程用来表示一条经过 $(x_0,y_0)$ 和 $(x_1,y_1)$ 的直线：改写下 $Ax+By=C$
- 证明如果矩阵的列是正交的，那么行也是如此：列向量正交 $\Leftrightarrow$ $\mathbf A^\mathrm T\mathbf A=\mathbf I$ $\Leftrightarrow$ $\mathbf A\mathbf A^\mathrm T=\mathbf I$ $\Leftrightarrow$ 行向量正交
- 略
- 略
- 略
- 证明 $\det(\vec a,\vec b,\vec c)=(\vec a\times\vec b)\cdot \vec c$：证明很简单，展开就行。比较常见，行列式表示三维空间中六面体的体积，而等式右侧叫做体积积，
- 四面体与六面体的体积之比是 $1:6$：底为 $1/2$，面积公式乘上 $1/3$，所以最后为 $1/6$
- 矩阵乘法的四种理解
- 略
- 略
- $A=\frac{1}{2}\begin{vmatrix}x_0 & x_1 & x_2\\y_0 & y_1 & y_2\\1 & 1 & 1\end{vmatrix}$：根据三角形面积公式 $A=\sqrt{p(p-a)(p-b)(p-c)}$（$p=\frac{a+b+c}{2}$）可以推出来