几何变换（Geometric transformations）可以通过矩阵乘法来实现
用于实现几何变换的矩阵称为变换矩阵（transformation matrices）
二维线性变换
$$ \begin{bmatrix}a_{11} & a_{12}\\a_{21} & a_{22}\end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix} =\begin{bmatrix}a_{11}x+a_{12}y\\a_{21}x+a_{22}y\end{bmatrix} $$上面的式子是对一个二维向量简单地进行矩阵乘，得到另一个二维向量，这种变换称为线性变换（linear transformation）
缩放（Scale）
沿着坐标轴缩放：
$$ \text {scale}(s_x,s_y)=\begin{bmatrix}s_x & 0\\0 & s_y\end{bmatrix}\\ \begin{bmatrix}s_x & 0\\0 & s_y\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}s_xx\\s_yy\end{bmatrix} $$剪切（Shear）
这里的剪切和我们理解的不同，剪切指的是把东西“推到一边”：
$$ \text {shear-x}(s)=\begin{bmatrix}1 & s\\0 & 1\end{bmatrix}\\ \text {shear-y}(s)=\begin{bmatrix}1 & 0\\s & 1\end{bmatrix} $$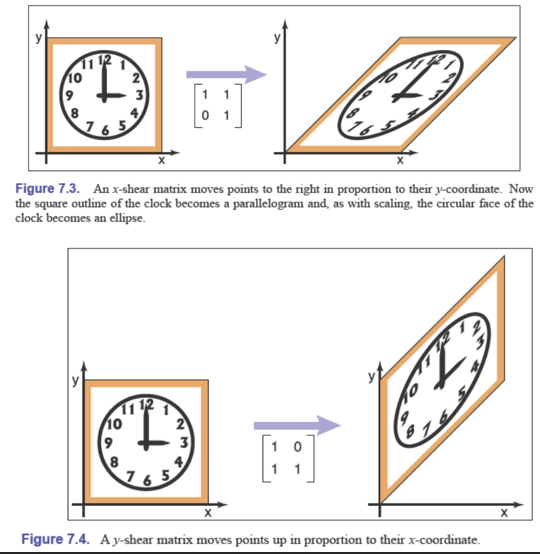
在上述剪切后，原先的正方形变成了平行四边形，圆变成了椭圆
另一种理解剪切变换的方法是“旋转”，将 $y$ 轴顺时针旋转 $\phi$ 角度的变换为：
$$ \begin{bmatrix}1 & \tan\phi\\0 & 1\end{bmatrix} $$将 $x$ 轴逆时针旋转 $\phi$ 角度的变换为：
$$ \begin{bmatrix}1 & 0\\\tan\phi & 1\end{bmatrix} $$旋转（Rotation）
假设我们现在有一个向量 $\vec a$，将其逆时针旋转 $\phi$ 角度得到向量 $\vec b$，设 $\vec a$ 与 $x$ 轴正方向夹角为 $\alpha$。
令 $r=\sqrt{x_a^2+x_b^2}$，那么：
$$ x_a=r\cos\alpha\\ y_a=r\sin\alpha $$旋转后 $r$ 不变，但是与 $x$ 轴正方向夹角变成了 $\alpha+\phi$，有：
$$ x_b=r\cos(\alpha+\phi)=r\cos\alpha\cos\phi-r\sin\alpha\sin\phi\\ y_b=r\sin(\alpha+\phi)=r\sin\alpha\cos\phi+r\cos\alpha\sin\phi $$然后我们就能得到（逆时针）旋转变换矩阵了：
$$ \text{rotate}(\phi)=\begin{bmatrix}\cos\phi & -\sin\phi\\\sin\phi & \cos\phi\end{bmatrix} $$旋转变换矩阵是正交矩阵
反转（Reflection）
$$ \text{reflect-y}=\begin{bmatrix}-1 & 0\\0 & 1\end{bmatrix}\\ \text{reflect-x}=\begin{bmatrix}1 & 0\\0 & -1\end{bmatrix} $$注意：反转和旋转的不同在于行列式是 $+1$ 还是 $-1$
如果 $x$ 轴和 $y$ 轴同时乘上 $-1$，那么行列式就变成了 $+1$，代表旋转 $\pi$ 角度
变换的合成与分解
特殊的例子：沿着某方向（非坐标轴）缩放，需要先旋转到坐标轴上，然后再缩放，最后转回去
相似对角化与奇异值分解
这里详细讲解了实对称矩阵的相似对角化、奇异值分解
实对称矩阵表示缩放变换
对于奇异值分解 $\mathbf A=\mathbf U\mathbf S\mathbf V^\mathrm T$（$\mathbf S$ 中的项用 $\sigma_i$ 表示），图解如下：
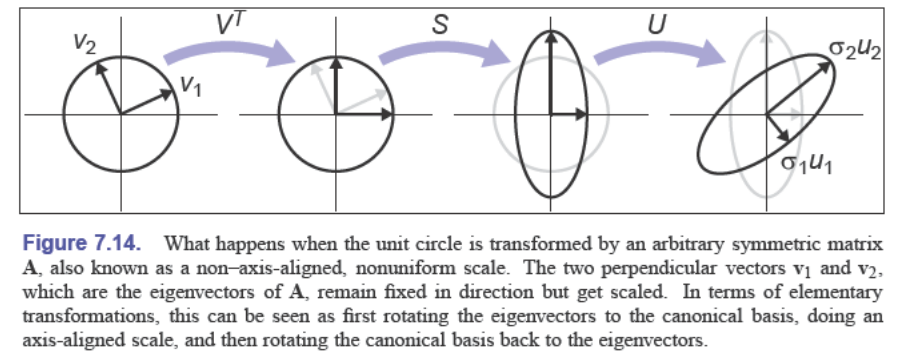
奇异值分解中对角矩阵是正的，但是 $\mathbf U$ 和 $\mathbf V$ 不一定对应旋转操作，也可能表示反转
当行列式为 $+1$ 是旋转，当行列式是 $-1$ 时是反转
如果需要旋转，则可以对奇异值取反来让 $\mathbf U$ 和 $\mathbf V$ 是旋转变换，把反转放在中间的缩放变换中
这样，所有矩阵都可以写成旋转矩阵乘缩放（或反转）矩阵，然后再乘一个旋转矩阵的形式
旋转矩阵的 paeth 分解
使用剪切（shear）来表示非零旋转：
$$ \text{rotate}(\phi)=\begin{bmatrix}\cos\phi & -\sin\phi\\\sin\phi & \cos\phi\end{bmatrix} =\begin{bmatrix}1 & \frac{\cos\phi-1}{\sin\phi}\\0 & 1\end{bmatrix} \begin{bmatrix}1 & 0\\\sin\phi & 1\end{bmatrix} \begin{bmatrix}1 & \frac{\cos\phi-1}{\sin\phi}\\0 & 1\end{bmatrix} $$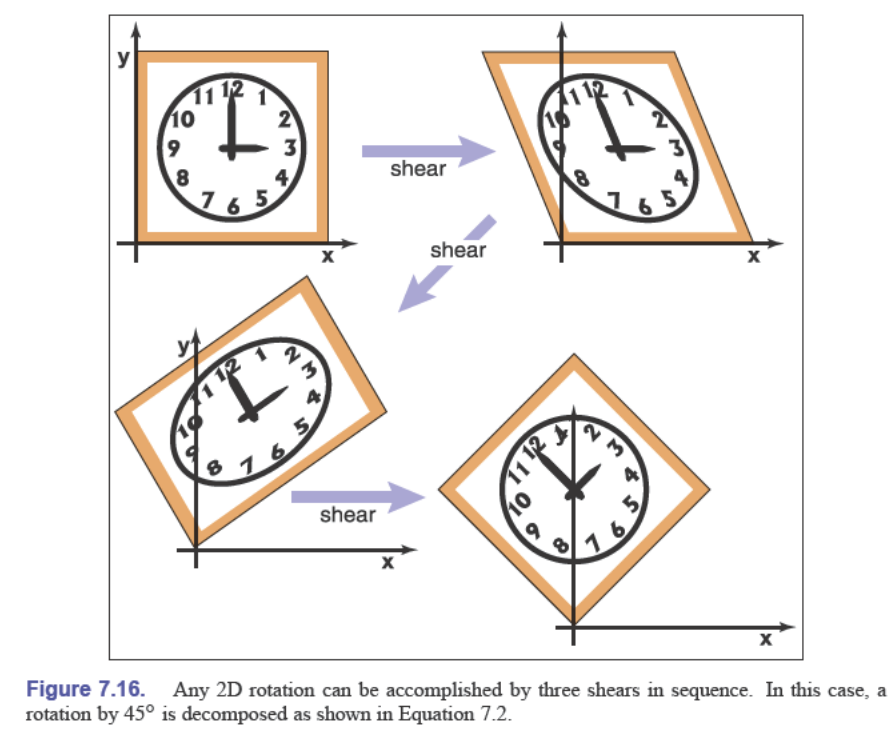
剪切是一种非常有用的光栅操作，它引入了锯齿，但不会留下缺口，看看怎么解释这句话：
对于光栅中的一个位置 $(i,j)$，如果对它进行水平剪切，得到：
$$ \begin{bmatrix}1 & s\\0 & 1\end{bmatrix}\begin{bmatrix}i\\j\end{bmatrix}=\begin{bmatrix}i+sj\\j\end{bmatrix} $$将 $sj$ 四舍五入后得到新坐标 $(i+\text{floor}(sj), j)$
相当于将原光栅的每一行横向移动，在同一行中，每个像素移动量相同，移动之后仍然是紧密排列的，所以说没有缺口
但是对于不同的行，它们移动量不同，所以在行与行之间会有相对的位移，所以说引入了锯齿
可以想象成一个一个方块（像素本来就是一个一个方块）
三维线性变换
缩放变换：
$$ \text{scale}(s_x,s_y,s_z)=\begin{bmatrix}s_x & 0 & 0\\0 & s_y & 0\\0 & 0 & s_z\end{bmatrix} $$沿着 $x$、$y$、$z$ 轴的旋转变换：
$$ \text{rotate-x}(\phi)=\begin{bmatrix}1 & 0 & 0\\0 & \cos\phi & -\sin\phi\\0 & \sin\phi & \cos\phi\end{bmatrix}\\ \text{rotate-y}(\phi)=\begin{bmatrix}\cos\phi & 0 & \sin\phi\\0 & 1 & 0\\-\sin\phi & 0 & \cos\phi\end{bmatrix}\\ \text{rotate-z}(\phi)=\begin{bmatrix}\cos\phi & -\sin\phi & 0\\\sin\phi & \cos\phi & 0\\0 & 0 & 1\end{bmatrix} $$注意对 $y$ 轴来说是沿着 $zOx$ 坐标系进行旋转而不是 $xOz$
剪切变换：
$$ \text{shear-x}(d_y,d_z)=\begin{bmatrix}1 & d_y & d_z\\0 & 1 & 0\\0 & 0 & 1\end{bmatrix} $$与二维相同，三维矩阵也可以进行奇异值分解，三维对称矩阵可以进行相似对角化，旋转矩阵可以进行 paeth 分解
沿着任意轴的旋转变换
对向量的旋转变换，是基变换的逆（如果可逆的话）
一组基底是 $\vec x$、$\vec y$、$\vec z$，另一组基底是 $\vec u$、$\vec v$、$\vec w$，其中：
$$ \vec u=a_{11}\vec x+a_{12}\vec y+a_{13}\vec z\\ \vec v=a_{21}\vec x+a_{22}\vec y+a_{23}\vec z\\ \vec w=a_{31}\vec x+a_{32}\vec y+a_{33}\vec z $$写成矩阵形式即：
$$ \begin{bmatrix}\vec x & \vec y & \vec z\end{bmatrix} \begin{bmatrix}a_{11} & a_{21} & a_{31}\\a_{12} & a_{22} & a_{32}\\a_{13} & a_{23} & a_{33}\end{bmatrix} =\begin{bmatrix}\vec u & \vec v & \vec w\end{bmatrix} $$表示成：
$$ \begin{bmatrix}\vec u & \vec v & \vec w\end{bmatrix}=\begin{bmatrix}\vec x & \vec y & \vec z\end{bmatrix}\mathbf A $$设有一个向量，在基底 $\vec x$、$\vec y$、$\vec z$ 下的坐标为 $(i,j,k)$，在基底 $\vec u$、$\vec v$、$\vec w$ 下的坐标为 $(i',j',k')$，则有：
$$ \begin{bmatrix}\vec u & \vec v & \vec w\end{bmatrix}\mathbf A^{-1}\begin{bmatrix}i\\ j\\ k\end{bmatrix} =\begin{bmatrix}\vec x & \vec y & \vec z\end{bmatrix}\begin{bmatrix}i\\ j\\ k\end{bmatrix} $$于是有：
$$ \begin{bmatrix}i'\\ j'\\ k'\end{bmatrix}=\mathbf A^{-1}\begin{bmatrix}i\\ j\\ k\end{bmatrix} $$如果我们考虑正交基，则 $\mathbf A^{-1}=\mathbf A^{\mathrm T}$
这里书上给出的方法是：
- 以旋转轴为 $w$ 轴，构造一个正交基 $\vec u$、$\vec v$、$\vec w$
- 我们知道向量在正交基 $\vec x$、$\vec y$、$\vec z$ 下的坐标 $(i,j,k)$，得到向量在新建的正交基下的坐标 $(i',j',k')$
- $(i',j',k')$ 沿着 $w$ 轴旋转得到旋转后的在 $\vec u$、$\vec v$、$\vec w$ 基底下的坐标
- 变换回在 $\vec x$、$\vec y$、$\vec z$ 基底下的坐标
我们从 $\vec x$、$\vec y$、$\vec z$ 旋转到 $\vec u$、$\vec v$、$\vec w$ 时，可以求得基变换矩阵 $\mathbf A$，即：
$$ \begin{bmatrix}\vec u & \vec v & \vec w\end{bmatrix}=\begin{bmatrix}\vec x & \vec y & \vec z\end{bmatrix}\mathbf A $$如果我们认为 $\vec x=(1,0,0)$、$\vec y=(0,1,0)$、$\vec z=(0,0,1)$，我们可以求出 $\mathbf A$：
$$ \begin{bmatrix}\vec u & \vec v & \vec w\end{bmatrix}=\mathbf I\mathbf A $$即：
$$ \mathbf A=\begin{bmatrix}\vec u & \vec v & \vec w\end{bmatrix} $$对于向量 $\vec \alpha=(i,j,k)$，求得 $\vec \beta=(i',j',k')$ 为：
$$ \vec\beta=\mathbf A^{-1}\vec\alpha $$然后将 $\vec \beta$ 绕着 $w$ 轴进行旋转得到旋转后的坐标 $\vec\beta'$：
$$ \vec \beta'=\mathbf R\mathbf A^{-1}\vec \alpha $$其中，旋转变换矩阵为：
$$ \mathbf R=\begin{bmatrix}\cos\phi & -\sin\phi & 0\\\sin\phi & \cos\phi & 0\\0 & 0 & 1\end{bmatrix} $$然后变换回 $\vec \alpha'$：
$$ \vec \alpha'=\mathbf A\mathbf R\mathbf A^{-1}\vec \alpha $$因为是正交基，所以可以写成：
$$ \vec \alpha'=\mathbf A\mathbf R\mathbf A^{\mathrm T}\vec \alpha $$代入并且展开我们可以得到绕着任一轴旋转的变换矩阵：
$$ \text{rotate}(\phi) =\begin{bmatrix}\vec u & \vec v & \vec w\end{bmatrix} \begin{bmatrix}\cos\phi & -\sin\phi & 0\\\sin\phi & \cos\phi & 0\\0 & 0 & 1\end{bmatrix} \begin{bmatrix}\vec u^\mathrm T \\ \vec v^\mathrm T \\ \vec w^\mathrm T\end{bmatrix} $$其中：
$$ \vec{w}=\frac{\vec{a}}{\Vert \vec{a}\Vert }\\ \vec{u}=\frac{\vec{t}\times\vec{w}}{\Vert \vec{t}\times\vec{w}\Vert }\\ \vec{v}=\vec{w}\times\vec{u} $$$\vec t$ 为任一与 $\vec w$ 不共线的向量
变换法向量
如果我们有一个变换矩阵 $\mathbf M$ 和一个曲面，当对曲面上的某点进行变换时，它的切线 $\vec t$ 乘上 $\mathbf M$ 后仍然是切线，但是法线 $\vec n$ 乘上 $\mathbf M$ 就不一定还是法线
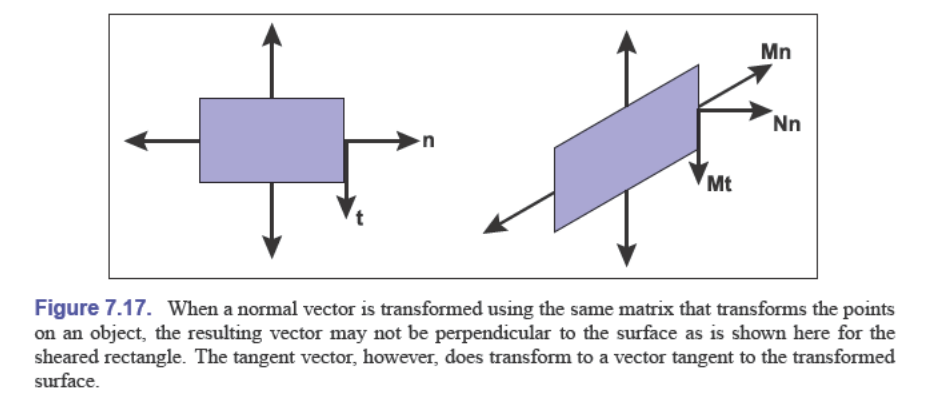
如何解决这个问题？
假设我们需要对法线向量乘上 $\mathbf N$，根据法线与切线垂直，我们有下面的式子：
$$ \vec n^\mathrm T\vec t=0 $$我们对切线左乘 $\mathbf M$，对法线左乘 $\mathbf N$，那么有：
$$ (\mathbf N\vec n)^\mathrm T\mathbf M\vec t=0\\ \vec n^\mathrm T\mathbf N^\mathrm T\mathbf M\vec t=0 $$注意到，当 $\mathbf N^\mathrm T\mathbf M=\mathbf I$ 时式子成立，那么：
$$ \mathbf N=(\mathbf M^{-1})^\mathrm T=\frac{1}{|\mathbf M|}(\mathbf M^{*})^\mathrm T $$如果我们不要求法线量的长度，那么我们可以忽略掉常数，即：
$$ \mathbf N=(\mathbf M^{*})^\mathrm T $$展开即：
$$ \mathbf N=[m_{ij}^c] $$平移（Translation）与仿射（Affine）变换
前面的都是线性变换，不能移动物体
一个可行的方法是每个矩阵关联一个平移向量，但是这样会很麻烦
有一个巧妙的技巧，就是增加一维，对二维来说，使用三维向量 $\begin{bmatrix}x&y&1\end{bmatrix}^\mathrm T$ 来表示平移量 $(x,y)$，如下：
$$ \mathbf M=\begin{bmatrix}m_{11} & m_{12} & x_t\\m_{21} & m_{22} & y_t\\0 & 0 & 1\end{bmatrix} $$变换如下：
$$ \begin{bmatrix}x'\\y'\\1\end{bmatrix}= \begin{bmatrix}m_{11} & m_{12} & x_t\\m_{21} & m_{22} & y_t\\0 & 0 & 1\end{bmatrix} \begin{bmatrix}x\\y\\1\end{bmatrix}=\begin{bmatrix}m_{11}x+m_{12}y+x_t\\m_{21}x+m_{22}y+y_t\\1\end{bmatrix} $$使用单个矩阵在线性变换后平移，这种变换称为仿射变换（affine transformation）
增加一维来实现仿射变换的方法叫做齐次坐标法（homogeneous coordinates）
当我们不需要位置这个信息（如方向向量或位移向量）时，可以把第三维变成 $0$ 而不是 $1$
之后，在透视视图（perspective viewing）中，齐次坐标不再是简单的 $0$ 或者 $1$，用处更大
齐次坐标是图形硬件设计和操作渲染器的基础
齐次坐标也可以有不同的解释，例如三维线性变换中的剪切变换
对于三维的也是如此，加一维变成四维
书上的例子是将矩形 $[x_l,x_h]\times[y_l,y_h]$ 变换到 $[x_l',x_h']\times[y_l',y_h']$
还有一个现象：
$$ \begin{bmatrix}1 & 0 & 0 & x_t\\0 & 1 & 0 & y_t\\0 & 0 & 1 & z_t\\0 & 0 & 0 & 1\end{bmatrix} \begin{bmatrix}a_{11} & a_{12} & a_{13} & 0\\a_{21} & a_{22} & a_{23} & 0\\a_{31} & a_{32} & a_{33}& 0\\0 & 0 & 0 & 1\end{bmatrix}=\begin{bmatrix}a_{11} & a_{12} & a_{13} & x_t\\a_{21} & a_{22} & a_{23} & y_t\\a_{31} & a_{32} & a_{33}& z_t\\0 & 0 & 0 & 1\end{bmatrix} $$也就是说：线性部分和平移部分可以彼此分离，合起来的话就等于先线性变换，再平移变换
注意反过来不行，不能先平移变换再线性变换
仿射变换的逆也是仿射变换的形式，这根据几何意义、线性代数计算都可以证明
坐标系变换
前面讨论过基变换，坐标系变换在基变换的基础上增加了原点的位移，如果坐标原点是 $\vec p$，基底为 $\vec u$、$\vec v$、$\vec w$，那么坐标 $(u,v,w)$ 表示的点是：
$$ \vec p=\vec e+u\vec u+v\vec v+w\vec w $$这个坐标可以通过齐次坐标来表示：
$$ \vec p=\begin{bmatrix}\vec u & \vec v & \vec w & \vec e \\ 0 & 0 & 0 & 1\end{bmatrix}\begin{bmatrix}u \\ v \\ w \\ 1\end{bmatrix} $$前面的基变换公式是：
$$ \begin{bmatrix}\vec u & \vec v & \vec w\end{bmatrix}=\begin{bmatrix}\vec x & \vec y & \vec z\end{bmatrix}\mathbf A $$延伸到坐标系变换中，使用齐次坐标系：
$$ \begin{bmatrix}\vec u & \vec v & \vec w & \vec e \\ 0 & 0 & 0 & 1\end{bmatrix}= \begin{bmatrix}\vec x & \vec y & \vec z & \vec o \\ 0 & 0 & 0 & 1\end{bmatrix}\mathbf A $$乘出来，我们发现 $\vec u$、$\vec v$、$\vec w$ 是 $\vec x$、$\vec y$、$\vec z$ 的线性组合（基变换部分），$\vec e$ 是 $\vec x$、$\vec y$、$\vec z$ 的线性组合加上 $\vec o$（在 $\vec o$ 的基础上平移）
对于基变换中的坐标变换，有：
$$ \begin{bmatrix}\vec u & \vec v & \vec w\end{bmatrix}\mathbf A^{-1}\begin{bmatrix}i\\ j\\ k\end{bmatrix} =\begin{bmatrix}\vec x & \vec y & \vec z\end{bmatrix}\begin{bmatrix}i\\ j\\ k\end{bmatrix} $$延伸到坐标系变换中，类似：
$$ \begin{bmatrix}\vec u & \vec v & \vec w & \vec e \\ 0 & 0 & 0 & 1\end{bmatrix}\mathbf A^{-1}\begin{bmatrix}i\\ j\\ k\\1\end{bmatrix} =\begin{bmatrix}\vec x & \vec y & \vec z & \vec o \\ 0 & 0 & 0 & 1\end{bmatrix}\begin{bmatrix}i\\ j\\ k\\1\end{bmatrix} $$所以：
$$ \begin{bmatrix}i'\\ j'\\ k'\\1\end{bmatrix}=\mathbf A^{-1}\begin{bmatrix}i\\ j\\ k\\1\end{bmatrix} $$有一个世界（全局）坐标系