基本变换
平移、旋转、缩放与剪切与它们的组合
平移：
$$ \mathbf T(\vec t)=\begin{bmatrix}1 & 0 & 0 & t_x\\0 & 1 & 0 & t_y\\0 & 0 & 1 & t_z\\0 & 0 & 0 & 1\end{bmatrix} $$旋转：
$$ \displaylines{ \mathbf R_x(\phi)=\begin{bmatrix}1 & 0 & 0 & 0\\0 & \cos\phi & -\sin\phi & 0\\0 & \sin\phi & \cos\phi & 0\\0 & 0 & 0 &1\end{bmatrix}\\ \mathbf R_y(\phi)=\begin{bmatrix}\cos\phi & 0 & \sin\phi & 0\\0 & 1 & 0 & 0\\-\sin\phi & 0 & \cos\phi & 0\\0 & 0 & 0 & 1\end{bmatrix}\\ \mathbf R_z(\phi)=\begin{bmatrix}\cos\phi & -\sin\phi & 0 & 0\\\sin\phi & \cos\phi & 0 & 0\\0 & 0 & 1 & 0\\0 & 0 & 0 & 1\end{bmatrix}} $$这三个旋转矩阵是正交矩阵
缩放：
$$ \mathbf S_x(\vec s)=\begin{bmatrix}s_x & 0 & 0 & 0\\0 & s_y & 0 & 0\\0 & 0 & s_z & 0\\0 & 0 & 0 &1\end{bmatrix} $$非均匀缩放（nonuniform）与均匀缩放（uniform）
各向同性（isotropic）和各向异性（anisotropic）
反射矩阵（reflection matrix）或镜像矩阵（mirror matrix）：向量 $\vec{s}$ 中包含 1 个或者 3 个为负的分量
如果有两个为负的分量，那么这个矩阵会将物体旋转 180 度（中心对称）
旋转矩阵和一个反射矩阵相乘，那么生成的结果仍将是一个反射矩阵
剪切：
$$ \mathbf H_{xz}(s)=\begin{bmatrix}1 & 0 & s & 0\\0 & 1 & 0 & 0\\0 & 0 & 1 & 0\\0 & 0 & 0 &1\end{bmatrix} $$任何剪切矩阵的行列式值都为 $\vert \mathbf{H} \vert =1$，这意味着剪切变换是一种体积保持（volume-preserving）的变换
变换的组合：
由于矩阵之间的乘法不具备交换律（noncommutativity），因此矩阵在乘法式子中的顺序十分重要
最常用的变换组合顺序是：
$$ \mathbf C=\mathbf T\mathbf R\mathbf S $$先缩放，再旋转，然后平移
刚体变换
只包含平移和旋转的变换叫做刚体变换（rigid-body transform），变换矩阵记作：
$$ \mathbf X=\mathbf T(\vec t)\mathbf R=\begin{bmatrix}\vec {r_{,0}}&\vec {r_{,1}}&\vec {r_{,2}}&\vec t\\0&0&0&1\end{bmatrix} $$它的逆是：
$$ \mathbf X^{-1}=\mathbf R^T\mathbf T(-\vec t)=\begin{bmatrix}\vec {r_{0}}&\vec {r_{1}}&\vec {r_{2}}&-\bar{\mathbf R}^T\vec t\\0&0&0&1\end{bmatrix} $$其中，$\bar{\mathbf R}$ 为 $\mathbf R$ 的左上角 $3 \times 3$ 子矩阵
法线变换
传统方法是使用：
$$ (\mathbf M^{-1})^T $$但是：
- 我们并不需要求出完整的逆矩阵，因为不需要第四维向量
- 有时候这个逆矩阵可能并不存在
我们只需要计算左上角 $3 \times 3$ 子矩阵的伴随矩阵，即可完成对法线的变换
如果表面法线是从变换之后的三角形中计算出来的话（例如使用三角形的边向量进行叉乘，从而获得垂直于三角形表面的法线），那么法线变换的问题就不需要进行考虑了
切向量的本质和法线并不相同，它可以直接使用原始变换矩阵进行变换
计算逆矩阵
根据变换的可用信息不同，我们可以使用以下三种方法来计算一个逆矩阵：
- 一次很简单的变换，或者是一系列带参简单变换的组合：直接根据物理意义求
- 正交矩阵：转置
- 什么信息都不知道：伴随矩阵法、Cramer 法则、LU 分解法、高斯消元法等，伴随矩阵法和 Cramer 法则通常要更好一些，因为它们所涉及的分支操作较少
在进行性能优化的时候，我们还可以对逆矩阵的计算目的进行考虑，例如：如果这个逆矩阵仅仅是用来对向量进行变换的话，那么通常我们只需要获得左上角 $3 \times 3$ 子矩阵的逆矩阵即可
特殊的矩阵变换和操作
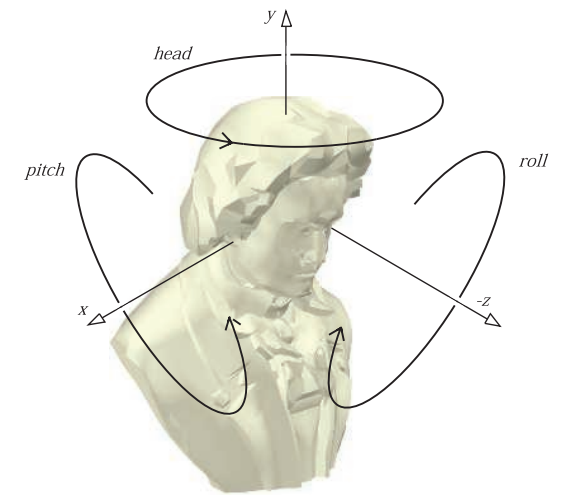
欧拉变换
欧拉变换可以构建一个旋转矩阵，将我们自身（相机）或者其他物体指向一个特定的方向，这是一种十分直观的方式
在图形学中，通常使用这样的组合方式来表示欧拉变换：
$$ \mathbf E(h,p,r)=\mathbf R_z(r)\mathbf R_x(p)\mathbf R_y(h) $$当然，它也是正交的
其中，$h$、$p$、$r$ 代表了每个方向（head 头部、pitch 俯仰角、roll 滚转角）上绕轴旋转的角度
有时，head 也可以叫做偏航角（yaw）
有时也可以把这三个角度都叫做 roll（x-roll、y-roll、z-roll）
欧拉角在小角度变化和调整观察者朝向方面十分有用，但是它也有一些严重的限制，即我们很难将两组欧拉角组合在一起。例如：在两组欧拉角之间进行插值，并不是简单地对每个分量分别进行插值就可以完成的
使用欧拉角也会导致一个叫做万向节死锁（gimbal lock）的问题
从欧拉变换中提取参数
在某些情况下，我们需要从一个代表欧拉变换的矩阵中，提取出各个方向上所改变的角度
我们设欧拉变换矩阵为：
$$ \mathbf{E}(h,p,r)=\begin{bmatrix}{} e_{00} & e_{01} & e_{02} \\ e_{10} & e_{11} & e_{12} \\ e_{20} & e_{21} & e_{22} \\ \end{bmatrix} $$我们将旋转矩阵代入欧拉角的表达式中并相乘可以得到：
$$ \mathbf{E}=\begin{bmatrix} \cos r \cos h - \sin r \sin p \sin h & - \sin r \cos p & \cos r \sin h + \sin r \sin p \cos h \\ \sin r \cos h + \cos r \sin p \sin h & \cos r \cos p & \sin r \sin h - \cos r \sin p \cos h \\ -\cos p \sin h & \sin p & \cos p \cos h \\ \end{bmatrix} $$观察发现：
$$ \displaylines{ e_{21}=\sin p\\ \frac{e_{01}}{e_{11}}=\frac{-\sin r}{\cos r}=-\tan r\\ \frac{e_{20}}{e_{22}}=\frac{-\sin h}{\cos h}=-\tan h } $$那么：
$$ \begin{aligned} h&=\text{atan2}(-e_{20},e_{22})\\ p&=\arcsin e_{21}\\ r&=\text{atan2}(-e_{01},e_{11}) \end{aligned} $$但是，我们需要处理一下 $\cos p=0$ 的问题，此时无法求出 $h$ 和 $r$
此时旋转角度 $r$ 和 $h$ 将会围绕着同一个旋转轴进行旋转（尽管它俩的旋转方向可能不同，这取决于旋转角度 $p$ 是 $-\pi/2$ 还是 $\pi/2$），在这种情况下，我们只需要计算其中任意一个角度即可
当 $p=-\pi/2$ 时，欧拉变换矩阵为：
$$ \begin{aligned} \mathbf{E}_{1}&=\begin{bmatrix} \cos r \cos h - \sin r \sin h & 0 & \cos r \sin h + \sin r \cos h \\ \sin r \cos h + \cos r \sin h & 0 & \sin r \sin h - \cos r \cos h \\ 0 & 1 & 0\end{bmatrix}\\ &=\begin{bmatrix} \cos (r+h) & 0 & \sin (r+h) \\ \sin (r+h) & 0 & \cos (r+h) \\ 0 & 1 & 0\end{bmatrix} \end{aligned} $$当 $p=\pi/2$ 时，欧拉变换矩阵为：
$$ \begin{aligned} \mathbf{E}_{1}&=\begin{bmatrix} \cos r \cos h + \sin r \sin h & 0 & \cos r \sin h - \sin r \cos h \\ \sin r \cos h - \cos r \sin h & 0 & \sin r \sin h + \cos r \cos h \\ 0 & -1 & 0\end{bmatrix}\\ &=\begin{bmatrix} \cos (r-h) & 0 & \sin (r-h) \\ \sin (r-h) & 0 & \cos (r-h) \\ 0 & -1 & 0\end{bmatrix} \end{aligned} $$观察发现，此时方程仅和 $r+h$ 或者 $r-h$ 有关，我们只需要假设其中一个旋转角度为 $0$，然后求出另一个即可
上面的这两种情况被称作万向节死锁（gimbal lock），即在旋转的过程中失去了一个自由度。
例如在上面的情况中，$p=\pm\pi/2+2\pi k$，此时整个矩阵只跟一个角度有关系，根据 $p$ 值的不同，这个角度可能是 $r+h$ 或者 $r-h$
在不同的系统中，通常都会使用不同的欧拉角顺序，例如：在动画中使用 $z$、$x$、$y$ 顺序，在动画和物理中也会使用 $z$、$x$、$z$ 顺序。没有任何一个顺序能够完美的避免万向节死锁问题，但是欧拉角仍然是最为常用的角度表示方法和旋转表示方法
矩阵分解
在总变换矩阵中分解出各种各样的子变换矩阵，这个过程叫做矩阵分解（matrix decomposition）
提取出平移矩阵是很简单的，我们只需要找到 $4 \times 4$ 矩阵中的最后一列元素即可
可以对变换矩阵的行列式进行检查，如果行列式的值是一个负数，那么就说明这个矩阵包含一个反射变换
而想要分离出旋转、缩放和剪切变换则需要更多的的努力
这里列了参考文献
绕任意轴旋转
如何从旋转轴 $\vec r$ 构建出一组正交基：
$$ \begin{aligned} \vec{s'}&=\cases{\begin{array}{ll}\left(0,-r_{z}, r_{y}\right), & \text { if }\left|r_{x}\right| \leq\left|r_{y}\right| \text { and }\left|r_{x}\right| \leq\left|r_{z}\right|, \\ \left(-r_{z}, 0, r_{x}\right), & \text { if }\left|r_{y}\right| \leq\left|r_{x}\right| \text { and }\left|r_{y}\right| \leq\left|r_{z}\right|, \\ \left(-r_{y}, r_{x}, 0\right), & \text { if }\left|r_{z}\right| \leq\left|r_{x}\right| \text { and }\left|r_{z}\right| \leq\left|r_{y}\right|\end{array}}\\ \vec{s}&=\frac{\vec{s'}}{\Vert \vec{s'}\Vert}\\ \vec{t}&=\vec{r} \times \vec{s} \end{aligned} $$其中，$\vec {s'}$ 的构建方法是：找到原始旋转轴 $\vec{r}$ 中的最小分量，然后将其设置为 $0$，再交换剩下两个分量的值，最后再将刚才两个不为 $0$ 的分量中的任意一个取反即可（这里先设置为 $0$，交换再取反的操作，实际上就是找到与旋转轴 $\vec{r}$ 同一平面的垂直向量）
还有一些其他的方法，例如 Frisvad 方法
然后我们就得到了基变换矩阵：
$$ \mathbf M=\begin{bmatrix}{} \vec{r}^T \\ \vec{s}^T \\ \vec{t}^T \end{bmatrix} $$然后，我们就可以得到绕归一化旋转轴 $\vec{r}$ 旋转 $\alpha$ 度的变换矩阵：
$$ \mathbf X(\vec r,\alpha)=\mathbf M^T\mathbf R_x(\alpha)\mathbf M $$这是一个正交矩阵
Goldman 还提出了另外一种绕任意归一化轴 $\vec{r}$ 旋转 $\phi$ 度的方法，这里我们直接将最终的变换矩阵展示出来：
$$ \mathbf R(\vec r,\phi)=\begin{bmatrix} \cos \phi+(1-\cos \phi) r_{x}^{2} & (1-\cos \phi) r_{x} r_{y}-r_{z} \sin \phi & (1-\cos \phi) r_{x} r_{z}+r_{y} \sin \phi \\ (1-\cos \phi) r_{x} r_{y}+r_{z} \sin \phi & \cos \phi+(1-\cos \phi) r_{y}^{2} & (1-\cos \phi) r_{y} r_{z}-r_{x} \sin \phi \\ (1-\cos \phi) r_{x} r_{z}-r_{y} \sin \phi & (1-\cos \phi) r_{y} r_{z}+r_{x} \sin \phi & \cos \phi+(1-\cos \phi) r_{z}^{2} \end{bmatrix} $$四元数
https://www.bilibili.com/video/BV14t421h7M4
四元数（quaternion）可以用于表示旋转和方向，它在很多地方都比欧拉角和矩阵表示更加优秀，它可以用于稳定且恒定速度的方向插值，这是欧拉角很难实现的。
它由四个部分组成，前三个值与旋转的轴有关，而旋转角度会对四个值都产生影响。每个四元数由四个实数表示，其中每个实数都对应了四元数的不同部分
四元数 $\hat q$ 的定义如下：
$$ \hat q=(\vec {q_v},q_w)=iq_x+jq_y+kq_z+q_w=\vec {q_v}+q_w $$其中，$i$、$j$、$k$ 有下面的关系：
$$ \displaylines{ i^2=j^2=k^2=-1\\ jk=-kj=i\\ ki=-ik=j\\ ij=-ji=k } $$$q_w$ 是四元数 $\hat q$ 的实数部分（实部），$\vec {q_v}$ 是 $\hat q$ 的虚数部分（虚部），$i$、$j$、$k$ 叫做虚数单位
四元数的结构和复数类似，但是复数只有一个虚部，而四元数则包含三个虚部
对于虚部 $\vec {q_v}$，我们可以将其看作为一个三维向量，可以对其应用诸如加法、缩放、点乘、叉乘以及其他的向量操作
注意：虚数单位之间的乘法不具备交换律
四元数的运算和性质
乘法：
$$ \begin{aligned} \hat q\hat r&=(iq_x+jq_y+kq_z+q_w)(ir_x+jr_y+kr_z+r_w)\\ &=i(q_yr_z-q_zr_y+r_wq_x+q_wr_x)+\dots+q_wr_w-q_xr_x-q_yr_y-q_zr_z\\ &=(\vec{q_v}\times\vec{r_v}+r_w\vec{q_v}+q_w\vec{r_v}-\vec{q_v}\cdot\vec{r_v}) \end{aligned} $$乘法不满足交换律
标量乘法：
$$ \displaylines{ s\hat q=(\vec 0,s)(\vec {q_v},q_w)=(s\vec {q_v},sq_w)\\ \hat qs=(\vec {q_v},q_w)(\vec 0,s)=(s\vec {q_v},sq_w) } $$可以看到，标量乘法满足交换律，即 $s\hat q=\hat qs$
加法：
$$ \hat q+\hat r=(\vec{q_v}+\vec{r_v},q_w+r_w) $$共轭：
$$ \hat q^*=(-\vec{q_v},q_w) $$模长：
$$ \begin{aligned} \Vert\hat q\Vert&=\sqrt{\hat q\hat q^*}=\sqrt{\hat q^*\hat q}=\sqrt{\vec{q_v}\cdot\vec{q_v}+q_w^2}\\ &=\sqrt{q_x^2+q_y^2+q_z^2+q_w^2} \end{aligned} $$单位元：
$$ \hat i=(\vec 0,1) $$单位元乘任何四元数仍然是该四元数本身
四元数的逆：
根据模长的计算，我们可以得到：
$$ \Vert\hat q\Vert^2=\hat q\hat q^*\Longleftrightarrow \frac{\hat q\hat q^*}{\Vert\hat q\Vert^2}=1 $$从而可以得到四元数的逆：
$$ \hat q^{-1}=\frac{1}{\Vert\hat q\Vert^2}\hat q^* $$共轭运算的性质：
$$ \displaylines{ (\hat q^*)^*=\hat q\\ (\hat q+\hat r)^*=\hat q^*+\hat r^*\\ (\hat q\hat r)^*=\hat r^*\hat q^* } $$模长运算的性质：
$$ \displaylines{ \Vert\hat q^*\Vert=\Vert\hat q\Vert\\ \Vert\hat q\hat r\Vert=\Vert\hat q\Vert\times\Vert\hat r\Vert } $$乘法分配律：
$$ \displaylines{ \hat p(s\hat q+t\hat r)=s\hat p\hat q+t\hat p\hat r\\ (s\hat p+t\hat q)\hat r=s\hat p\hat r+t\hat q\hat r } $$乘法结合律：
$$ \hat p(\hat q\hat r)=(\hat p\hat q)\hat r $$单位四元数
单位四元数（unit quaternion）的模长为 $1$，因此我们可以把单位四元数改写成如下形式：
$$ \hat q=(\vec {u_q}\sin\phi,\cos\phi)=\vec {u_q}\sin\phi+\cos\phi $$其中，$\vec{u_q}$ 是一个单位向量
对于复数而言，一个二维单位向量可以被写成 $\cos \phi + i\sin \phi = e^{i \phi}$ 的形式（复变函数中的欧拉公式），而对于一个四元数来说，其等价形式如下：
$$ \hat q=\vec {u_q}\sin\phi+\cos\phi=e^{\phi\vec{u_q}} $$根据这个式子，我们可以得到单位四元数 $\hat q$ 的对数运算和幂运算式子：
幂运算：
$$ \hat q^t=(\vec {u_q}\sin\phi,\cos\phi)^t=e^{\phi t\vec{u_q}}=\vec{u_q}\sin(\phi t)+\cos(\phi t) $$对数运算：
$$ \log\hat q=\log e^{\phi\vec{u_q}}=\phi\vec{u_q} $$代入前面的四元数逆的公式，我们可以得到单位四元数的逆：
$$ \hat q^{-1}=\frac{1}{\Vert\hat q\Vert^2}\hat q^*=q^* $$四元数变换
我们现在将研究四元数中的一个子集，即单位四元数（unit quaternion），单位四元数可以用于表示任何的三维旋转，而且这种表示方式非常紧凑和简单
假设我们有单位四元数 $\hat q=\vec u_q\sin\phi+\cos\phi$，有一个点 $\vec p$，我们将 $\vec p$ 的四个分量放到 $\hat p$ 的四个分量中，进行如下操作：
$$ \hat q\hat p\hat q^{-1}=\hat q\hat p\hat q^{*} $$这相当于把 $\hat p$ 以 $\vec u_q$ 为旋转轴，旋转 $2\phi$ 角度，并且发现 $\hat q$ 与 $-\hat q$ 表示的旋转变换一样
变换可以进行组合，例如：
$$ \hat r(\hat q\hat p\hat q^{*})\hat r^*=(\hat r\hat q)\hat p(\hat r\hat q)^*\equiv\hat c\hat p\hat c^* $$矩阵转换
四元数 $\hat q$ 可以转换为变换矩阵 $\mathbf M^q$：
$$ \mathbf{M}^{q}=\begin{bmatrix}1-s\left(q_{y}^{2}+q_{z}^{2}\right) & s\left(q_{x} q_{y}-q_{w} q_{z}\right) & s\left(q_{x} q_{z}+q_{w} q_{y}\right) & 0 \\ s\left(q_{x} q_{y}+q_{w} q_{z}\right) & 1-s\left(q_{x}^{2}+q_{z}^{2}\right) & s\left(q_{y} q_{z}-q_{w} q_{x}\right) & 0 \\ s\left(q_{x} q_{z}-q_{w} q_{y}\right) & s\left(q_{y} q_{z}+q_{w} q_{x}\right) & 1-s\left(q_{x}^{2}+q_{y}^{2}\right) & 0 \\ 0 & 0 & 0 & 1\end{bmatrix} $$其中， $s=2 /(n\hat q)^{2}$。对于一个单位四元数而言，可以将其化简为：
$$ \mathbf{M}^{q}=\begin{bmatrix}1-2\left(q_{y}^{2}+q_{z}^{2}\right) & 2\left(q_{x} q_{y}-q_{w} q_{z}\right) & 2\left(q_{x} q_{z}+q_{w} q_{y}\right) & 0 \\ 2\left(q_{x} q_{y}+q_{w} q_{z}\right) & 1-2\left(q_{x}^{2}+q_{z}^{2}\right) & 2\left(q_{y} q_{z}-q_{w} q_{x}\right) & 0 \\ 2\left(q_{x} q_{z}-q_{w} q_{y}\right) & 2\left(q_{y} q_{z}+q_{w} q_{x}\right) & 1-2\left(q_{x}^{2}+q_{y}^{2}\right) & 0 \\ 0 & 0 & 0 & 1\end{bmatrix} $$上述转换方程中不包含任何三角函数运算，因此这个转换在实际应用中是很高效的
正交矩阵 $\mathbf M^q$ 也可以反向转换为单位四元数 $\hat q$，根据上面的转换方程找规律作差，可得：
$$ \begin{aligned} m_{21}^q-m_{12}^q&=4q_wq_x\\ m_{02}^q-m_{20}^q&=4q_wq_y\\ m_{10}^q-m_{01}^q&=4q_wq_z \end{aligned}\tag{1} $$然后，我们发现：
$$ \mathrm{tr}(\mathbf M^q)=\frac{4q_w^2}{(n\hat q)^2} $$然后，我们就能得到：
$$ \begin{aligned} m_{00} &=t+2 q_{x}^{2}, \\ m_{11} &=t+2 q_{y}^{2}, \\ m_{22} &=t+2 q_{z}^{2}, \\ m_{00}+m_{11}+m_{22}&=t+2 q_{w}^{2}, \end{aligned}\tag{2} $$其中，$t=q_w^2-q_x^2-q_y^2-q_z^2$，我们能进一步得到：
$$ \begin{aligned} 4 q_{x}^{2}&=+m_{00}-m_{11}-m_{22}+m_{33}\\ 4 q_{y}^{2}&=-m_{00}+m_{11}-m_{22}+m_{33}\\ 4 q_{z}^{2}&=-m_{00}-m_{11}+m_{22}+m_{33}\\ 4 q_{w}^{2}&=\operatorname{tr}\left(\mathbf{M}^{q}\right) \end{aligned}\tag{3} $$总而言之，方程 2 可以用来计算四元数虚部分量 $q_{x},q_{y},q_{z}$ 中的哪一项最大，根据最大项的不同，适当选取方程 3 中的一个来计算这个最大分量，最后使用方程 1 来计算 $\hat{q}$ 的其余分量。
球面线性插值
对于参数 $t\in[0,1]$，球面线性差值的表达式为：
$$ \hat s(\hat q,\hat r,t)=(\hat r\hat q^{-1})^t\hat q $$但是通常使用更为合适的 slerp 函数来代替球面线性插值：
$$ \mathrm{slerp}(\hat q,\hat r,t)=\frac{\sin\left(\phi(1-t)\right)}{\sin\phi}\hat q+\frac{\sin(\phi t)}{\sin\phi}\hat r $$其中，$\cos\phi=q_xr_x+q_yr_y+q_zr_z+q_wr_w$
slerp 插值具有恒定速度，绕着固定的旋转轴绕一个大圆
球面立方插值（Spherical cubic interpolation）
将一个向量旋转到另一个向量
如果我们想要将方向 $\vec s$ 以最短路径变换到另一个方向 $\vec t$，我们可以用四元数来简化这个过程：
$$ \hat q=\left(\frac{\vec s\times\vec t}{\sqrt{2(1+e)}},\frac{\sqrt{2(1+e)}}{2}\right) $$其中，$e=\vec s\cdot\vec t$。上面的式子就是找到一个旋转轴 $\vec s\times\vec t$，然后计算旋转角度
使用这种方式构建四元数（相比于对叉积 $\vec{s} \times \vec{t}$ 的结果进行标准化），避免了当 $\vec{s}$ 和 $\vec{t}$ 几乎指向相同方向时造成的数值不稳定。但是当 $\vec s$ 和 $\vec t$ 指向相反方向时，$e=-1$，两种方法都会出现数值不稳定的情况，此时可以使用任何一个垂直于 $\vec s$ 的向量作为旋转轴，然后再旋转
矩阵形式：
$$ \mathbf{R}(\vec{s}, \vec{t})=\begin{bmatrix}e+h v_{x}^{2} & h v_{x} v_{y}-v_{z} & h v_{x} v_{z}+v_{y} & 0 \\ h v_{x} v_{y}+v_{z} & e+h v_{y}^{2} & h v_{y} v_{z}-v_{x} & 0 \\ h v_{x} v_{z}-v_{y} & h v_{y} v_{z}+v_{x} & e+h v_{z}^{2} & 0 \\ 0 & 0 & 0 & 1\end{bmatrix} $$其中：
$$ \begin{aligned} \vec{v} &=\vec{s} \times \vec{t} \\ e &=\cos (2 \phi)=\vec{s} \cdot \vec{t} \\ h & =\frac{1-\cos (2 \phi)}{\sin ^{2}(2 \phi)} =\frac{1-e}{\vec{v} \cdot \vec{v}} =\frac{1}{1+e} \end{aligned} $$当 $\phi \approx 0$ 的时候，我们可以返回单位矩阵。当 $2 \phi \approx \pi$ 时，我们可以绕任意轴旋转 $\pi$ 弧度
顶点混合和模型的变形
顶点混合（vertex blending）是一种解决非刚体变换中关节灵活柔韧（flexible）问题的常见方法
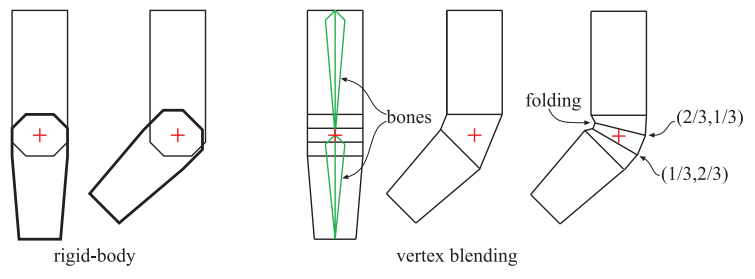
我们可以允许单个顶点被若干个不同的矩阵所变换，并将这些变换所得到的结果加权混合在一起。这是通过为动画物体设置一个骨架来完成的
顶点混合非常适合在 GPU 上运行，我们可以将网格中的顶点集合放入 GPU 的静态缓存中（只需要发送一次），之后重复使用这个缓存即可。使用一个顶点着色器，来计算骨骼节点对缓存中存储网格的影响。可以将骨骼的变换存储在顶点可以访问的纹理（四元数）中
双四元数混合（dual quaternion）、旋转中心蒙皮（center-of-rotation）
变形目标（morph target）或者形状混合（blend shape）、姿态空间变形技术（pose-space deformation）
投影
规范化设备坐标系（normalized device coordinates，NDC；也叫做齐次裁剪空间）
有一些方法可以用来提高深度值的精度，其中反向 z-buffer（reversed z）是一种比较常用的方法
当使用浮点数据来表示 z-buffer 的时候，存储 $1-z_{\mathrm{NDC}}$ 的值；当使用整数来表示 z-buffer 的时候，反向存储 $z_{\mathrm{NDC}}$ 的值
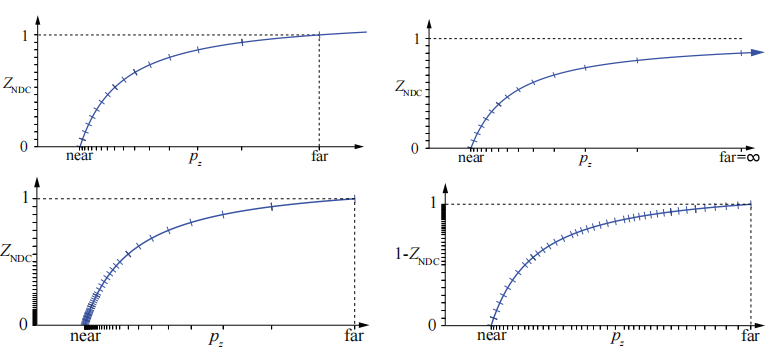
上图中，第二行是使用浮点数表示的，可以看到反向 z-buffer（右下角）确实分布表现良好