纹理管线

纹理化（texturing）是一种用于描述表面材质以及对表面进行修饰加工的有效技术

图像纹理中的像素通常被称为纹素（texel）

粗糙度纹理、凹凸纹理

投影函数（projector function）：将空间中的三维坐标转换为二维纹理坐标

纹理坐标（texture coordinates）：将纹理坐标转换为纹理空间中的具体位置

纹理映射（texture mapping）

转换函数（corresponder function）：来将纹理坐标转换到纹理空间中，例如把 $[0,1]$ 转化成 $[0, 256)$

值转换函数（value transform function）：转换检索到的纹理值，例如颜色值从三通道转换成四通道

针对单个纹理的广义纹理管线：

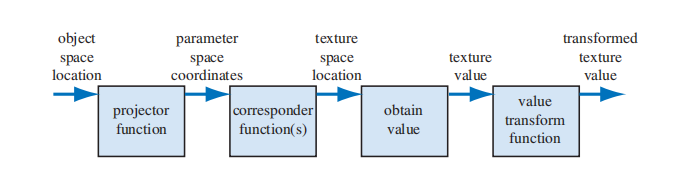
投影函数

常用的投影函数包括球面投影（spherical）、柱面投影（cylindrical）和平面投影（planar）

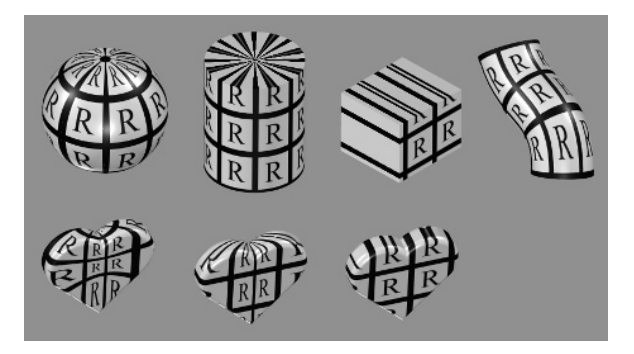
分 UV、网格参数化（mesh parameterization）

方向性的贴图，可以放到单位球体上。一个例子是立方体贴图（cube map）

在进行插值之前，这些纹理坐标还需要使用转换函数进行变换

转换函数

提高了在表面上应用纹理的灵活性，例如它可以用来选择现有纹理中的一个子图像来进行显示

一类转换函数是矩阵变换，它们允许对表面上的纹理进行平移、旋转、缩放、剪切或者投影操作。变换顺序与预期顺序相反

另一类控制了图像的应用方式，包装模式（wrapping mode，OpenGL）、纹理寻址模式（texture addressing mode，DirectX），常见的有：

• wrap（DirectX），repeat（OpenGL）或 tile：图像会在表面上进行重复，整数部分会被直接丢弃
• mirror：图像在表面上不断重复，但是每重复一次就会被镜像（翻转）一次
• clamp（DirectX）或 clamp to edge（OpenGL）
• border（DirectX）或 clamp to border（OpenGL）：$[0,1]$ 之外的会被赋予边框颜色（border color）
• mirror once（DirectX）：对纹理只进行一次镜像操作，然后再使用 clamp 模式

每个纹理轴上所分配的转换函数可以是不同的

纹理的重复平铺是一种为场景添加更多视觉细节的廉价方法，但是通常来说，这种方法在纹理重复三次之后就看起来不太自然了，因为人眼会识别出这种重复的图案。避免这种周期性（periodicity）问题的方法：

• 将纹理值与另一个非重复平铺的纹理相结合
• 使用着色器程序来实现一些特殊的转换函数，从而将纹理图案和 tile 贴图进行随机重组

最后一类转换函数是隐式的，并且与图像的大小有关，就是 $[0,1]$ 乘上分辨率

纹理值

最直接的纹理值就是 RGB 三元组，还可以加上 alpha 通道

纹理贴图中不仅仅可以存储颜色数据，还可以存储任何其他类型的数据，例如表面粗糙度等

从纹理中返回的值可以在使用之前进行选择性地转换，这些转换一般都是在着色器程序中执行的。例如：从 $[0,1]$ 映射到 $[-1,1]$ 从而可以存储法线数据

图像纹理

依赖纹理读取（dependent texture read）有两个定义：

• 在像素着色器内修改了传入的纹理坐标。对于移动端和老 GPU 来说，在没有依赖纹理读取的情况下会具有更高的效率，因为纹理数据可以被预先读取
• 一个纹理坐标依赖于之前的纹理值结果。如一个纹理可能会改变表面的着色法线，这反过来又会改变用于访问立方体贴图（cube map）的坐标。这样的操作会对性能产生影响

GPU 所使用的纹理尺寸通常为 $2^m ×2^n$，其中 $m$ 和 $n$ 为非负整数，这样的纹理叫做二次幂（power-of-two，POT）纹理

现代 GPU 可以处理任意大小的非二次幂（NPOT）纹理，但是一些老旧的移动端 GPU 可能并不支持 NPOT 纹理的 mipmap

不同的图形加速器对于纹理尺寸有着不同的上限

放大（Magnification）

最常见的放大过滤技术是：

• 邻近过滤（nearest neighbor，实际使用了 box 滤波器）
• 双线性插值（bilinear interpolation）
• 三次卷积插值（cubic convolution）或者叫双三次插值（bicubic interpolation）：使用了 $4\times 4$ 或者 $5\times 5$ 范围纹素的加权和

下面三个图片依次为邻近过滤、双线性过滤、立方滤波（双三次插值）：

细节贴图（detail texture）：一种用于解决放大模糊的常见方法。这个纹理代表了表面上的精细细节，例如手机上的划痕和地形上的灌木丛等。这些细节会作为一个独立的纹理贴图，以不同的尺度被覆盖在放大后的纹理上。

下图是双线性插值中纹理的重新映射（分别为邻近过滤、双线性插值和部分重新映射的结果）：

双三次插值（bicubic filter）比双线性插值的计算成本更高，但是许多的高阶滤波器都可以被表示为重复的线性插值，因此可以通过若干次简单的线性插值，来充分利用纹理单元中用于线性插值操作的 GPU 硬件

可以在在一组 $2\times 2$ 纹素之间，使用平滑曲线进行插值，最长用的两个平滑曲线分别是 smoothstep 曲线和 quintic（五次）曲线：

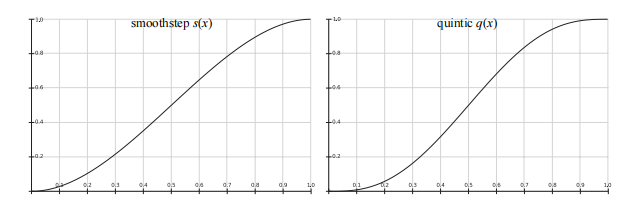
这种方法会原本 $(u,v)$ 减去 $0.5$ 后的小数部分 $(u',v')$ 先转换成 $\left(q(u'),q(v')\right)$，然后再加 $0.5$ 和原来的整数部分，重新传给 GPU 进行双线性插值查找

对比图（邻近过滤、线性差值、quintic 曲线、三次插值）：

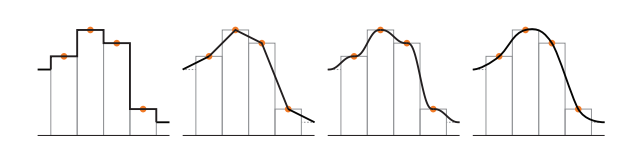
缩小（Minification）

最简单的就是邻近过滤（nearest neighbor），直接选择位于像素单元中心可见的纹素值，来作为自身的像素值。会产生严重的锯齿问题

当表面相对于相机发生移动的时候，这种瑕疵会变得更加明显，这种在运动中所产生的瑕疵也被称为时域锯齿（temporal aliasing）

另一个常用的滤波器是双线性插值，只比邻近过滤稍微好一点

根据奈奎斯特定理（Nyquist），只需要确保纹理的信号频率不大于采样频率的一半，就能避免走样和锯齿。我们要么提高像素的采样频率（前面的抗锯齿方法），要么降低纹理的信号频率，因此提出了各种纹理缩小算法

所有纹理抗锯齿算法的基本思想都是：对纹理进行预处理，创建某种数据结构，从而快速近似计算出一组纹素对像素的影响

Mipmap

Mip 是拉丁语 multum in parvo 的缩写，它的意思是“一个很小的地方上有很多东西”

原始纹理图像会生成一系列较小尺寸的版本，原始图像作为第 0 级别子纹理，一直对上一级别进行 $2\times 2$ 的下采样生成当前级别的子纹理，直到最后大小为 1

图片的几何称为一个 mipmap 链：

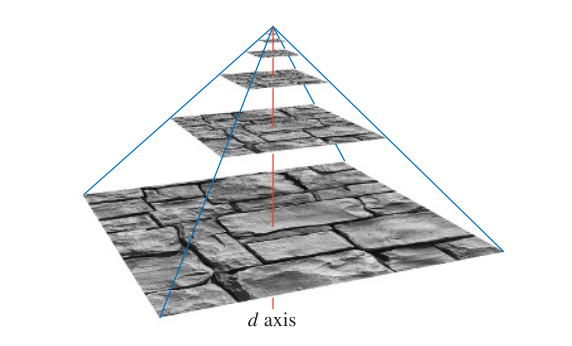
生成 mipmap 的常用方法是进行平均，即一个 $2\times 2$ 的 box 滤波器。

但是效果不好，最好使用高斯、Lanczos、Kaiser 或者类似的过滤器

在靠近纹理边缘进行过滤的时候的地方，需要注意纹理的 wrapping mode

对于在非线性颜色空间中进行编码的纹理（例如大多数的彩色纹理，sRGB 纹理），需要先转换到线性颜色空间，然后再生成 mipmap，否则物体会越来越暗

使用 mipmap 时，纹理坐标会有三维：$(u,v,d)$，其中都非整数，计算第三个纹理坐标 $d$（OpenGL 叫做 $\lambda$，纹理细节级别，texture level of detail）有两种方法：

• 使用像素投影的四边形，选择较长的边来近似
• 使用四个梯度 $\frac{\partial u}{\partial x}$、$\frac{\partial v}{\partial x}$、$\frac{\partial u}{\partial y}$、$\frac{\partial v}{\partial y}$ 中最大的那个作为度量。梯度在像素着色器中计算，不能在受动态流程控制的部分访问梯度信息（GPU 不会主动存储 uv 值，只会在相邻像素都执行 ddy 和 ddx 时才能得到相邻像素的 uv 值）

最后得到的纹理坐标进行三线性插值（trilinear interpolation）：使用坐标 $(u, v)$ 来从这两个 mipmap 中分别进行双线性插值，获得两个纹理值。最后按照参数 $d$ 再对这两个纹理值进行一次线性插值

可以通过细节层次偏移（level of detail bias，LOD bias）来对坐标 $d$ 进行一定的控制

mipmap 也存在缺陷：

• 过度模糊（overblurring）：不同方向上的纹素覆盖情况不同

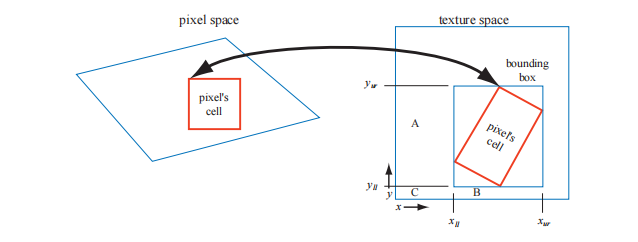
Summed-Area 表（SAT）

另一种能够避免过度模糊的方法是面积积分表（summed-area table，SAT，也可以叫做求和面积表）

首先要创建一个尺寸与纹理相同的数组，但是颜色存储的精度要更高（如每个通道占 16 位），因为要存储前缀和

就是右上角的前缀和减去左下角的前缀和，如图：

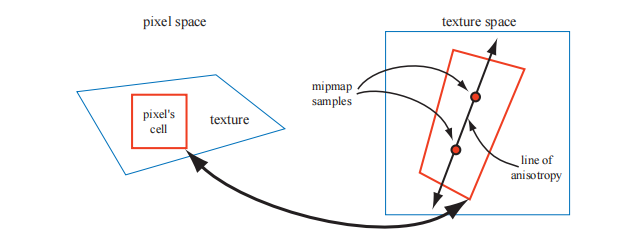
无约束的各向异性过滤

使用四边形中较短的那个边来确定 $d$ 的值，而四边形的长边则被用来创建一条与其平行，并且穿过四边形中点的各向异性线（line of anisotropy）

然后沿着这条线根据各向异性比例取若干个样本，如图：

椭圆加权平均（Elliptical Weighted Average，EWA）滤波器

立方体贴图（Cube Map）

具有六个正方形的纹理，立方体的六个面分别对应了这个六个正方形纹理

访问立方体贴图需要使用一个包含三个分量的纹理坐标向量，这个向量代表了从立方体中心向外发射的射线方向

首先看射线会射到哪个表面，这可以简单地通过最大分量来确定，例如 $(-3.2,5.1,-8.4)$ 会射向 $-z$ 面

然后再将其重新映射到 $[0,1]$ 上，这可以通过除以最大分量的绝对值来得到：

例如 $(-3.2,5.1,-8.4)$ 的直线方程是 $\vec p=t(-3.2,5.1,-8.4)^T$，直接用 $-1$ 除以 $-8.4$ 就能得到 $t$，然后就能得到 $[-1,1]$ 内的坐标，然后再重新映射到 $[0,1]$ 内即可

注意，这里其实不要求这个方向向量是单位向量

纹理表示

本小节重点是纹理图集（texture atlas）、纹理数组（texture array）以及无绑定的纹理（bindless textures），所有这些技术的目的都是为了在渲染过程中避免纹理的切换。后面还会介绍纹理流（texture streaming）和纹理转码（texture transcoding）

纹理图集（左，9 个小图像被组合为一个大纹理）和纹理数组：

图集中子纹理的形状和尺寸可以是任意的，它有一些问题：

• 在生成和访问图集 mipmap 的时候需要格外当心，图集中的子纹理可能会与另一个子纹理相互混合
• 当使用 wrapping/repeat 或者 mirror 模式的时候，无法使用纹理图集

对于上述的这些问题，一个更简单的解决方案是使用一种被称为纹理数组（texture array）的 API 结构

一个纹理数组中的所有子纹理都需要具有相同的尺寸、格式、mipmap 层次结构和 MSAA 设置

如果没有无绑定纹理，纹理会存在 GPU 的纹理单元中，数量有上限

无绑定纹理（bindless texture）使得纹理的使用数量是没有上限的，它放在显存中，通过句柄来与其数据结构相关联。可以通过多种方式来访问这些句柄，例如通过 uniform buffer、可变数据、其他纹理，以及着色器存储缓冲对象（shader storage buffer object，SSBO）等

纹理压缩

固定压缩比的纹理压缩（fixed-rate texture compression）是一种直接解决内存、带宽以及缓存问题的解决方案

S3 纹理压缩是 DirectX 的标准纹理压缩方法，被称为 DXTC，后面也称为 BC（块压缩，Block Compression），它也是 OpenGL 事实上的标准

DXTC/BC 压缩方案在 $4\times 4$ 范围内的纹素块（也称为 tile）上完成，每个纹素块都可以进行单独编码。这个编码过程是基于插值的，对于每个 tile 只会存储两个颜色和一个索引值，然后在两个颜色的直线上按照索引值插值一个颜色

优点：快速解码、随机访问、无间接查找和固定压缩比

有七个变体，下图给了它们的：

• 所占空间：Storage 列，前面的值表示每个 tile 所占字节数，后面的值表示每个纹素所占的比特数，即 bits per texel
• 存储的颜色格式：Ref colors 列，RGB565 表示三个通道依次占用 5、6、5 比特，乘 2 表示存储两个颜色
• 索引所占空间：Indices 列
• alpha 通道采取的方案：Alpha 列，有的是存储原始值（raw），有的是插值（interp）

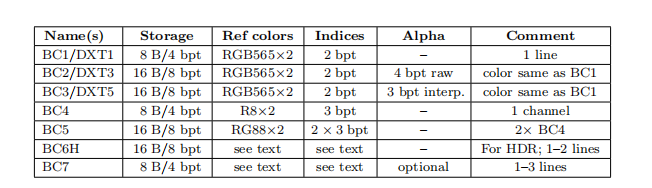
这里看看就行了

OpenGL ES 选择了另一种压缩算法，被称为 Ericsson 纹理压缩（Ericsson texture compression，ETC），该方案具有与S3TC相同的特点

它将 $4\times 4$ 的纹素块编码为 64 比特，即每个像素使用 4 比特，每 $2\times 4$ 块存储一个基色（base color），然后它有一个很小的常量表，每个纹素可以选择其中的四个常量，加上基色

在 OpenGL ES 3.0 中使用了 ETC2

法线贴图的压缩需要注意一些问题，它需要满足单位向量的限制，我们完全可以让 $z$ 向量为正，然后只需要存储两个分量 $x$ 和 $y$ 即可，$z$ 可以计算出来

然后我们用 BC5 或者 3Dc 压缩格式来压缩 $x$ 和 $y$ 分量（剩下看不懂了）

PVRTC 也是一种纹理压缩格式，它可以在 Imagination Technologies 的硬件（叫做 PowerVR）上使用

自适应可伸缩纹理压缩（Adaptive scalable texture compression，ASTC）

它们都是有损压缩。数据压缩的不对称性（data compression asymmetry）：数据的压缩过程要比解压过程花费更长的时间

程序化纹理

目前的 GPU 架构正在向着更低的计算成本，以及更昂贵（相对）的存储访问发展，存储访问和带宽限制越来越成为 GPU 的性能瓶颈。这些趋势使得程序化纹理在实时渲染中得到了更加广泛的应用

体积纹理是程序化纹理的一个特别有吸引力的应用，最为常见的一种方法是：使用一个或者多个噪声函数来生成纹理值

这些噪声函数通常都是以连续 2 次幂的频率进行采样的，这被称为 octave（八度）。每个 octave 都有一个权重，这个权重通常会随着频率的增加而下降，而这些加权样本的总和被称为湍流（turbulence）函数

由于计算噪声函数的成本较大，因此三维数组中的点通常都是预先计算好的，并使用这些点进行插值从而获得相应的纹理值

其他的程序化方法也是可行的，例如：蜂窝状纹理（cellular texture）

另一种类型的程序化纹理是物理模拟或者其他交互过程的结果，可以根据动态条件的不同，有效地生产无限种变化

当生成一个程序化的二维纹理时，参数化问题（UV）可能要比创建纹理更加困难。一种解决方案是直接在表面上合成纹理，从而完全避免参数化的问题。但是在复杂表面执行这种操作具有挑战性

对程序化纹理的抗锯齿处理，要比图像纹理的抗锯齿既困难和又容易，有各种各样的抗锯齿

纹理动画

纹理和纹理坐标不一定是静态的

可以通过对纹理坐标应用变换矩阵来生成更加精细的效果。除了平移之外，它还允许其他的线性变换操作，例如缩放、旋转和剪切，图像扭曲（image warping）和变形转换（morphing transforms），以及广义投影等

纹理混合（texture blending）：几个纹理按照某种比例混合

材质映射

纹理的一个常见用途是对材质属性进行修改，从而影响着色方程的计算结果。像素着色器可以从纹理中读取纹理值，并在计算着色方程之前，使用它们来修改材质的参数

纹理最常修改的参数就是表面颜色，这种纹理通常被称为反照率颜色贴图（albedo color map）或者漫反射颜色贴图（diffuse color map）

纹理还可以用来控制像素着色器本身的流程以及函数功能，而不是简单地修改着色方程中的参数

在具有生锈区域的金属表面上，可以使用一个特殊纹理来指示生锈的位置，根据纹理查找的结果，来决定是执行哪个着色器

对于包含非线性着色输入参数的纹理而言（如粗糙度或者凹凸贴图），需要更多的注意和处理来避免锯齿和走样。使用将着色方程考虑在内的滤波技术，可以改善这类纹理的结果

Alpha 映射