《Fundamentals of Computer Graphics》8. Viewing

之前的章节中，矩阵变换是在三维或二维世界中排列对象的工具，矩阵变换的另一个重要用途是在“三维世界的二维视角”中的位置和三维世界中的位置进行转换

3D 到 2D 的映射叫做视图变换（viewing transformation），视口变换在对象顺序渲染中很重要，因为我们要频繁地查找每个对象在 2D 中的位置

第四章中，学习了不同类型的透视、正交视图以及如何生成观察射线。

本章是第四章的逆过程，本章将阐述如何使用矩阵变换来描述“平行视图”和“透视视图”，本章中的变换会将 3D 场景中的点投影到图像中的 2D 点，并且会将给定像素的观察射线上的任意点投影回像素的位置

把三维世界中的点投影到二维，仅仅能够做到线框（wireframe）的渲染，即物体边缘。距离摄像机更近的面不会遮挡更远的面

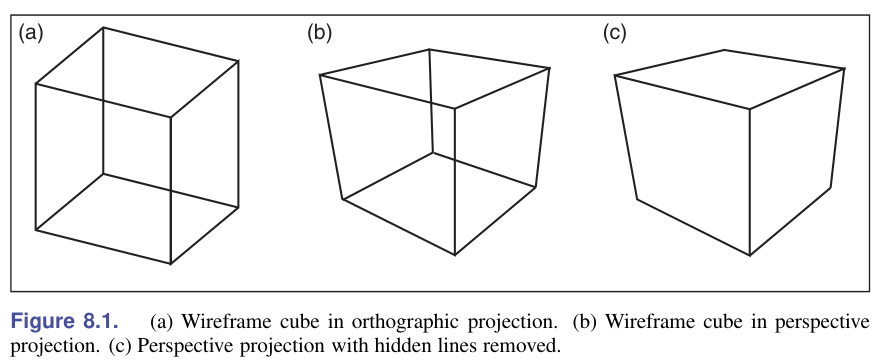
也就是这一章仅仅是线框的渲染，之后的章节会讨论对象表面的渲染

视图变换（Viewing Transformations）

视图变换的任务是将 3D 坐标 $(x, y, z)$ 映射到图像中的坐标（以像素为单位）

这是个复杂的过程，取决于摄像机的位置和方向、投影类型、视野、图像的分辨率等

与所有复杂的变换一样，最好将其分解为几个更简单的变换的乘积。大多数图形系统通过使用三个变换序列来实现这一点：

相机变换（camera transformation）或视变换（eye transformation）：将相机放置在原点，并且朝向方便计算的方向（例如 $x$ 轴正方向？）。这一步仅取决于相机的位置、方向或者叫姿态（pose）
投影变换（projection transformation）：将三维场景中的点映射到相机空间（camera space），所有点将在 $x$ 和 $y$ 方向上都落到 $- 1$ 到 $1$ 的范围内。这一步仅取决于投影类型
视口变换（viewport transformation）或窗口变换（windowing transformation）：将单位图像矩形映射到像素坐标系的矩形。这一步仅取决于输出图像的大小和位置

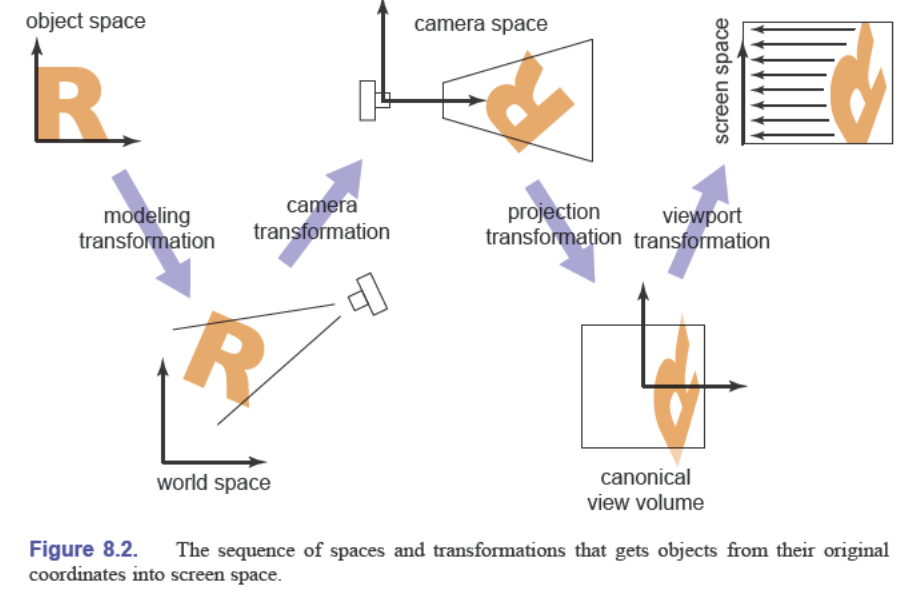
摄像机坐标系（camera coordinates）、摄像机空间（camera space）

规范视空间（canonical view volume）： $(x, y, z) \in [- 1, 1]^{3}$ 的一个正方体， $x = - 1$ 和 $x = 1$ 代表屏幕的最左侧和最右侧， $y = - 1$ 和 $y = 1$ 分别代表屏幕的最下边和最上边

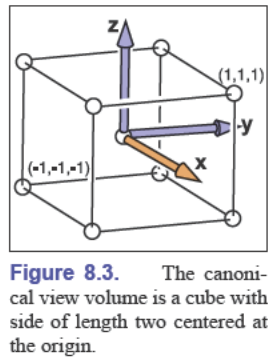
视口变换（Viewport Transformation）

从规范视空间映射到屏幕空间（screen space），即将 $[- 1, 1]^{2}$ 映射到 $[- 0.5, n_{x} - 0.5] \times [- 0.5, n_{y} - 0.5]$

假设现在所有线段都在规范视空间内部，之后在讨论剪切（clipping）时，会放松这个限制

上一章有一个例子，提供了一个公式，如下：

\begin{matrix} x^{'} = n_{x} \frac{x + 1}{2} - 0.5 \\ y^{'} = n_{y} \frac{y + 1}{2} - 0.5 \end{matrix}

写成矩阵形式：

[\begin{matrix} x_{screen} \\ y_{screen} \\ 1 \end{matrix}] = [\begin{matrix} \frac{n_{x}}{2} & 0 & \frac{n_{x} - 1}{2} \\ 0 & \frac{n_{y}}{2} & \frac{n_{y} - 1}{2} \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} x_{canonical} \\ y_{canonical} \\ 1 \end{matrix}]

我们把 $z$ 坐标加进来（之后的章节会进行深度测试），得到视口（变换）矩阵（viewport matrix）：

M_{vp} = [\begin{matrix} \frac{n_{x}}{2} & 0 & 0 & \frac{n_{x} - 1}{2} \\ 0 & \frac{n_{y}}{2} & 0 & \frac{n_{y} - 1}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

注意，这里好像有点问题：屏幕像素大小是 $n_{x} \times n_{y}$ ，那么整数表示的屏幕空间应该是 $[0, n_{x} - 1] \times [0, n_{y} - 1]$ ，所以屏幕空间应该是 $[- 0.5, n_{x} - 1.5] \times [- 0.5, n_{y} - 1.5]$

所以视口变换应该是：

M_{vp} = [\begin{matrix} \frac{n_{x}}{2} & 0 & 0 & \frac{n_{x} - 3}{2} \\ 0 & \frac{n_{y}}{2} & 0 & \frac{n_{y} - 3}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

正交投影矩阵

这里的正交投影应该指的是平行正交投影，最简单的一种，只需要垂直移动到图像上就可以了

首先，将视线方向的方向记作 $- z$ 方向（与左手系、右手系有关），并且 $y$ 轴朝上

然后，框一个长方体 $[l, r] \times [b, t] \times [f, n]$

构成的空间被称为正交视图空间（orthographic view volume）

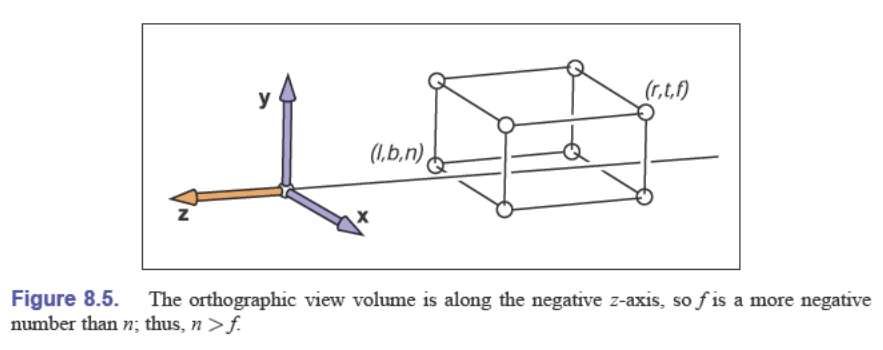
从正交视图空间到规范视空间的变换很简单：

x^{'} = \frac{x - \frac{l + r}{2}}{\frac{r - l}{2}} = \frac{2 x - (r + l)}{r - l}

写成矩阵就是：

M_{orth} = [\begin{matrix} \frac{2}{r - l} & 0 & 0 & - \frac{r + l}{r - l} \\ 0 & \frac{2}{t - b} & 0 & - \frac{t + b}{t - b} \\ 0 & 0 & \frac{2}{n - f} & - \frac{n + f}{n - f} \\ 0 & 0 & 0 & 1 \end{matrix}]

从正交视图空间到屏幕空间变换就是把上面得到的两个矩阵相乘，即：

[\begin{matrix} x_{screen} \\ y_{screen} \\ z_{canonical} \\ 1 \end{matrix}] = M_{vp} M_{orth} [\begin{matrix} x \\ y \\ z \\ 1 \end{matrix}]

$z$ 轴现在在 $[- 1, 1]$ 区间内，之后使用 z-buffer 进行深度测试时需要

画线段的伪代码：

construct M_vp
construct M_orth
M = M_vp M_orth
for each line-segment (a_i, b_i) do
    p = M a_i
    q = M b_i
    drawline(x_p, y_p, x_q, y_q)

相机变换（Camera Transformation）

相机变换就是世界空间到相机空间的变换

有许多约定用于指定相机的位置和方向。我们将使用以下一种：

眼睛的位置 $\vec{e}$
注视方向（gazing direction） $\vec{g}$
相机的向上向量 $\vec{t}$

通过这三个向量来构建一个坐标系

首先构建一个正交基：

\begin{matrix} \vec{w} = - \frac{\vec{g}}{‖ \vec{g} ‖} \\ \vec{u} = \frac{\vec{t} \times \vec{w}}{‖ \vec{t} \times \vec{w} ‖} \\ \vec{v} = \vec{w} \times \vec{u} \end{matrix}

然后加上位移 $\vec{e}$ ，根据上一章的坐标系变换，我们可以得到变换矩阵：

M_{cam} = {[\begin{matrix} \vec{u} & \vec{v} & \vec{w} & \vec{e} \\ 0 & 0 & 0 & 1 \end{matrix}]}^{- 1} = {[\begin{matrix} x_{u} & x_{v} & x_{w} & x_{e} \\ y_{u} & y_{v} & y_{w} & y_{e} \\ z_{u} & z_{v} & z_{w} & z_{e} \\ 0 & 0 & 0 & 1 \end{matrix}]}^{- 1}

上一章中说，仿射变换可以分解成线性变换和平移变换，它可以写成：

M_{cam} = {([\begin{matrix} 1 & 0 & 0 & x_{e} \\ 0 & 1 & 0 & y_{e} \\ 0 & 0 & 1 & z_{e} \\ 0 & 0 & 0 & 1 \end{matrix}] [\begin{matrix} x_{u} & x_{v} & x_{w} & 0 \\ y_{u} & y_{v} & y_{w} & 0 \\ z_{u} & z_{v} & z_{w} & 0 \\ 0 & 0 & 0 & 1 \end{matrix}])}^{- 1}

其中，我们知道左上的坐标系变换是正交矩阵（因为它就是由三个正交向量组成），所以后面矩阵的逆可以很轻松地求出来

前面的矩阵是平移变换，所以根据数学意义也可以轻松求出

所以：

M_{cam} = [\begin{matrix} x_{u} & y_{u} & z_{u} & 0 \\ x_{v} & y_{v} & z_{v} & 0 \\ x_{w} & y_{w} & z_{w} & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] [\begin{matrix} 1 & 0 & 0 & - x_{e} \\ 0 & 1 & 0 & - y_{e} \\ 0 & 0 & 1 & - z_{e} \\ 0 & 0 & 0 & 1 \end{matrix}]

画线段的伪代码：

construct M_vp
construct M_orth
construct M_cam
M = M_vp M_orth M_cam
for each line-segment (a_i, b_i) do
    p = M a_i
    q = M b_i
    drawline(x_p, y_p, x_q, y_q)

投影变换（Projective Transformations）

对于透视投影，我们要把空间中的点映射到规范视空间中，我们会用到 $z$ 坐标，并且 $z$ 坐标在分母上，如下（仅仅是举例子，并不是真的是这样）：

y_{s} = \frac{d}{z} y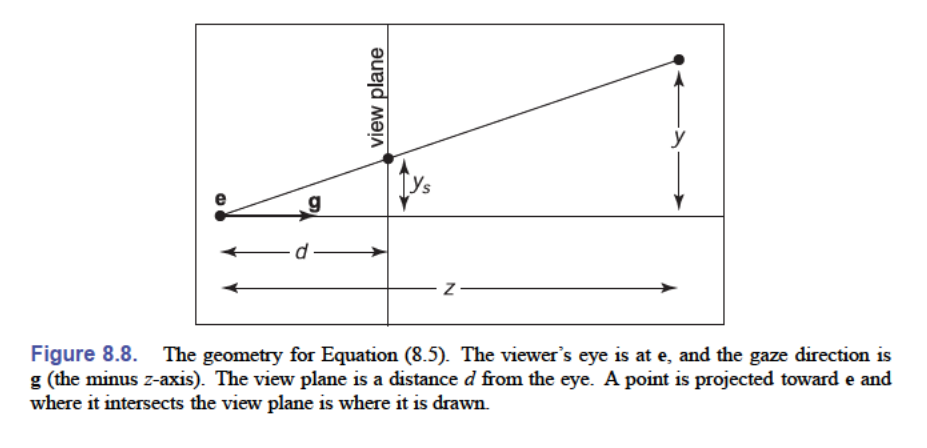

传统的矩阵变换做不到这样（除法）

我们使用一个简单的方法推广齐次坐标的机制来进行除法：

对于之前的齐次坐标， $(x, y, z)$ 表示为 ${[\begin{matrix} x & y & z & 1 \end{matrix}]}^{T}$ ，多出来的一维永远是 $1$ ，且仿射变换矩阵中的第四行永远是 $[\begin{matrix} 0 & 0 & 0 & 1 \end{matrix}]$

现在，我们让第四维是 $w$ ， ${[\begin{matrix} x & y & z & w \end{matrix}]}^{T}$ 用来表示坐标 $(x / w, y / w, z / w)$ ，这对之前没有影响（因为除以 $1$ 没什么意义）

线性变换允许我们计算：

\begin{matrix} x^{'} = a_{1} x + b_{1} y + c_{1} z \\ y^{'} = a_{2} x + b_{2} y + c_{2} z \\ z^{'} = a_{3} x + b_{3} y + c_{3} z \end{matrix}

仿射变换允许我们计算：

\begin{matrix} x^{'} = a_{1} x + b_{1} y + c_{1} z + d_{1} \\ y^{'} = a_{2} x + b_{2} y + c_{2} z + d_{2} \\ z^{'} = a_{3} x + b_{3} y + c_{3} z + d_{3} \end{matrix}

将 $w$ 作为分母允许我们计算：

\begin{matrix} x^{'} = \frac{a_{1} x + b_{1} y + c_{1} z + d_{1}}{e x + f y + g z + h} \\ y^{'} = \frac{a_{2} x + b_{2} y + c_{2} z + d_{2}}{e x + f y + g z + h} \\ z^{'} = \frac{a_{3} x + b_{3} y + c_{3} z + d_{3}}{e x + f y + g z + h} \end{matrix}

但是，还有一个限制，就是 $x$ 、 $y$ 、 $z$ 的除数相同

表示成矩阵形式如下：

[\begin{matrix} \tilde{x} \\ \tilde{y} \\ \tilde{z} \\ \tilde{w} \end{matrix}] = [\begin{matrix} a_{1} & b_{1} & c_{1} & d_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} \\ a_{3} & b_{3} & c_{3} & d_{3} \\ e & f & g & h \end{matrix}] [\begin{matrix} x \\ y \\ z \\ 1 \end{matrix}]

并且：

(x^{'}, y^{'}, z^{'}) = (\tilde{x} / \tilde{w}, \tilde{y} / \tilde{w}, \tilde{z} / \tilde{w})

这样的变换称为投影变换（projective transformation）或者单应变换（homography）

有一种更优雅的方式来解释 $w$ 坐标：3D 投影变换视作 4D 线性变换，并且额外规定：

\vec{x} \sim α \vec{x}, α \neq 0

这表示两个齐次坐标 $\vec{x}$ 与 $α \vec{x}$ （ $α \neq 0$ ）是同一个三维空间中的点

这些点构成了一条直线

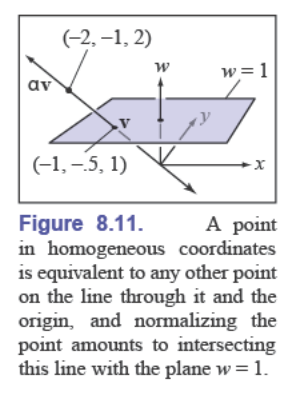
在需要笛卡尔坐标时，只需要找到它和 $w = 1$ 这个面上的交点就可以了

其实就是说给齐次向量乘上一个倍数不影响它表示的坐标

透视投影

使用投影变换后，前面的 $y_{s}$ 表达式可以写成：

[\begin{matrix} y_{s} \\ 1 \end{matrix}] \sim [\begin{matrix} d & 0 & 0 \\ 0 & 1 & 0 \end{matrix}] [\begin{matrix} y \\ z \\ 1 \end{matrix}]

根据惯例，在相机空间中，相机朝向 $- z$ 方向，近屏幕和远平面为 $n$ 与 $f$ （都是负数），使用这样的变换：

\begin{matrix} x^{'} = \frac{n x}{z} \\ y^{'} = \frac{n y}{z} \\ z^{'} = \frac{(n + f) z - f n}{z} = n + f - \frac{f n}{z} \end{matrix}

为什么 $z$ 坐标不能直接使用呢？因为实现不了 $z^{'} = z^{2} / z$ 的操作，只能通过相似的变换来实现。

规范视空间是 $[- 1, 1]^{3}$ ，为什么 $z$ 坐标没有映射到 $[- 1, 1]$ 上？因为这不是到规范视空间的变换，还要再乘上一个前面得到的 $M_{orth}$

上面是最常用的一种变换，它保证了当 $z = n$ 和 $z = f$ 时有 $z^{'} = z = n$ 和 $z^{'} = z = f$

写成矩阵形式为：

P = [\begin{matrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n + f & - f n \\ 0 & 0 & 1 & 0 \end{matrix}]

这个矩阵被称为透视矩阵（perspective matrix）

变换为：

P [\begin{matrix} x \\ y \\ z \\ 1 \end{matrix}] = [\begin{matrix} n x \\ n y \\ (n + f) z - f n \\ z \end{matrix}] \sim [\begin{matrix} n x / z \\ n y / z \\ n + f - f n / z \\ 1 \end{matrix}]

我们看一下 $P$ 的逆：

P^{- 1} = [\begin{matrix} \frac{1}{n} & 0 & 0 & 0 \\ 0 & \frac{1}{n} & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & - \frac{1}{f n} & \frac{n + f}{f n} \end{matrix}]

由于乘上一个系数没有影响，我们乘上一个 $f n$ ，它的逆可以写成：

P^{- 1} = [\begin{matrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 0 & f n \\ 0 & 0 & - 1 & n + f \end{matrix}]

我们乘上 $M_{orth}$ 之后就是透视投影矩阵（perspective projection matrix），注意是左乘：

M_{per} = M_{orth} P

一个问题是如何确定 $M_{orth}$ 所需的 $l$ 、 $r$ 、 $b$ 、 $t$ ，我们知道透视矩阵变换后，在 $z = n$ 面上 $x$ 与 $y$ 坐标不会改变，所以可以在这里确定 $l$ 、 $r$ 、 $b$ 、 $t$

相乘之后 $M_{per}$ 长这样：

M_{per} = [\begin{matrix} \frac{2 n}{r - l} & 0 & \frac{l + r}{l - r} & 0 \\ 0 & \frac{2 n}{t - b} & \frac{b + t}{b - t} & 0 \\ 0 & 0 & - \frac{f + n}{f - n} & \frac{2 f n}{f - n} \\ 0 & 0 & 1 & 0 \end{matrix}]

在 OpenGL 中，它会让我们指定 $| n |$ 和 $| f |$

其他的图像 API 中，通常将 $n$ 设置为 $0$ ，将 $f$ 设置为 $1$

规范视空间有时还会设置为 $[0, 1]^{3}$

上面的决策都会改变投影矩阵

变换线段的伪代码：

construct M_vp
construct M_per
construct M_cam
M = M_vp M_per M_cam
for each line-segment (a_i, b_i) do
    p = M a_i
    q = M b_i
    drawline(x_p, y_p, x_q, y_q)

透视变换的一些性质

直线性

一个重要性质是将线转换为线，将平面转换为平面，另外将线段转换为线段，例如，我们有这样的线段：

\vec{f} (t) = \vec{q} + t (\vec{Q} - \vec{q})

对它进行透视变换：

\begin{aligned} \vec{g} (t) & = M_{per} (\vec{q} + t (\vec{Q} - \vec{q})) \\ = M_{per} \vec{q} + t (M_{per} \vec{Q} - M_{per} \vec{q}) \\ \equiv \vec{r} + t (\vec{R} - \vec{r}) \end{aligned}

如果没有同质化，那么肯定存在线性关系，且 $t$ 不变，所以有：

w_{g} = w_{r} + t (w_{r} - w_{r})

经过同质化后， $\vec{g} (t)$ 、 $\vec{r}$ 、 $\vec{R}$ 变成了：

\begin{matrix} \vec{g} (t) \to \frac{\vec{r} + t (\vec{R} - \vec{r})}{w_{r} + t (w_{r} - w_{r})} \\ \vec{r} \to \frac{\vec{r}}{w_{r}} \\ \vec{R} \to \frac{\vec{R}}{w_{R}} \end{matrix}

其中，我们如果可以找到一个线性关系：

\frac{\vec{r} + t (\vec{R} - \vec{r})}{w_{r} + t (w_{r} - w_{r})} = \frac{\vec{r}}{w_{r}} + t^{'} (\frac{\vec{R}}{w_{R}} - \frac{\vec{r}}{w_{r}})

我们就可以知道：原来是一条直线上的点，经过透视变换并同质化后仍然在一条直线上

进行一些操作：

\begin{aligned} \frac{\vec{r} + t (\vec{R} - \vec{r})}{w_{r} + t (w_{R} - w_{r})} & = \frac{(1 - t) \vec{r} + t \vec{R}}{(1 - t) w_{r} + t w_{R}} \\ = \frac{(1 - t) w_{r}}{(1 - t) w_{r} + t w_{R}} \frac{\vec{r}}{w_{r}} + \frac{t w_{R}}{(1 - t) w_{r} + t w_{R}} \frac{\vec{R}}{w_{R}} \\ = [1 - \frac{t w_{R}}{(1 - t) w_{r} + t w_{R}}] \frac{\vec{r}}{w_{r}} + \frac{t w_{R}}{(1 - t) w_{r} + t w_{R}} \frac{\vec{R}}{w_{R}} \\ = \frac{\vec{r}}{w_{r}} + \frac{t w_{R}}{(1 - t) w_{r} + t w_{R}} (\frac{\vec{R}}{w_{R}} - \frac{\vec{r}}{w_{r}}) \\ \equiv \frac{\vec{r}}{w_{r}} + t^{'} (\frac{\vec{R}}{w_{R}} - \frac{\vec{r}}{w_{r}}) \end{aligned}

如果我们表示成 $\vec{g_{h}} (t)$ 、 $\vec{r_{h}}$ 、 $\vec{R_{h}}$ ，那么总结一下，有：

\vec{f} (t) = \vec{q} + t (\vec{Q} - \vec{q})

经过透视变换后：

\vec{g} (t) = \vec{r} + t (\vec{R} - \vec{r})

然后经过同质化后：

\vec{g_{h}} (t) = \vec{r_{h}} + t^{'} (\vec{R_{h}} - \vec{r_{h}})

其中：

t^{'} = \frac{t w_{R}}{(1 - t) w_{r} + t w_{R}}

我们发现确实是这样，而且， $t^{'} = f (t)$ 是个连续函数，确保不会被“撕裂（torn）”

视野（Field-of-View）

虽然我们可以使用 $l$ 、 $r$ 、 $b$ 、 $t$ 来指定窗口，但是有一个更简单的方法：从窗口的中心观察，即 $l = - r$ ， $b = - t$

这样的话只需要两个自由度就能表示这个窗口

如果我们添加了这样一个约束：

\frac{n_{x}}{n_{y}} = \frac{r}{t}

来表示“图像的性质没有失真”，即二者比例相同。

一旦二者比值被指定，那么还需要一个自由度就可以表示这个窗口了，通常使用视野来指定：

\tan \frac{θ}{2} = \frac{t}{| n |}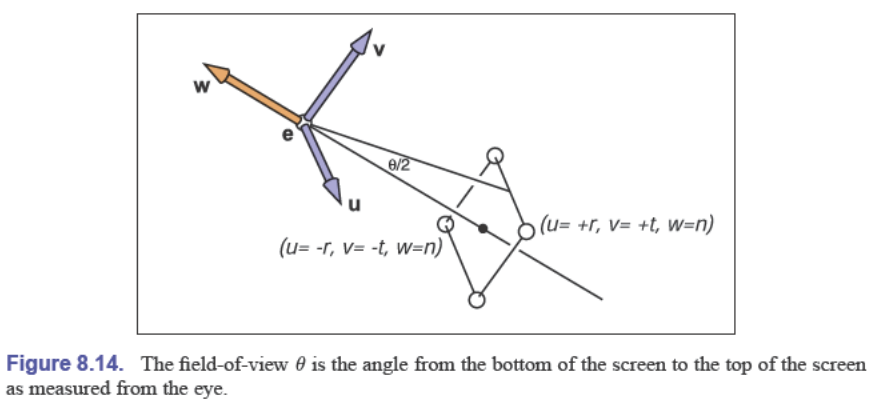

在某些系统中， $n$ 被硬编码成一个合理的定值，那么我们只需要知道 $θ$ 就可以计算出 $t$ 了

问题和练习

在透视矩阵中：

z^{'} = n + f - \frac{n f}{z}

当有一个线段，它跨越了 $z = 0$ 时会发生撕裂，即 $a / 0 = \infty$ ， $a / - 0 = - \infty$ ，这通常可以使用剪切来避免，但是撕裂现象使剪切本身变得更加复杂，之后会讨论

在透视变换之后，需要把 $w$ 坐标变成 $1$

构建视口矩阵，其中像素坐标从图像顶部向下计数：
$\begin{matrix} x^{'} = n_{x} \frac{1 + x}{2} - 0.5 = \frac{n_{x} x + n_{x} - 1}{2} \\ y^{'} = n_{y} \frac{1 - y}{2} - 0.5 = \frac{- n_{y} y + n_{y} - 1}{2} \end{matrix}$
那么矩阵为：
$M_{vp} = [\begin{matrix} \frac{n_{x}}{2} & 0 & 0 & \frac{n_{x} - 1}{2} \\ 0 & - \frac{n_{y}}{2} & 0 & \frac{n_{y} - 1}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]$
视口矩阵与正交矩阵相乘的意义是：一个长方体映射到正方体，再将 $x$ 与 $y$ 坐标映射到屏幕空间。两个操作合在一起就是将 $[l, r] \times [b, t] \times [n, f]$ 映射到 $[- 0.5, n_{x} - 0.5] \times [- 0.5, n_{y} - 0.5] \times [- 1, 1]$
略
从代数角度证明透视矩阵保留了视场内的 $z$ 值顺序。略
略
略
略
略
略
使用前面的办法构建正交基即可？
根据 $f (t)$ 很容易证